Lý thuyết Phương trình quy về phương trình bậc hai - SGK Toán 10 Kết nối tri thứcA. Lý thuyết 1. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \) Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Quảng cáo
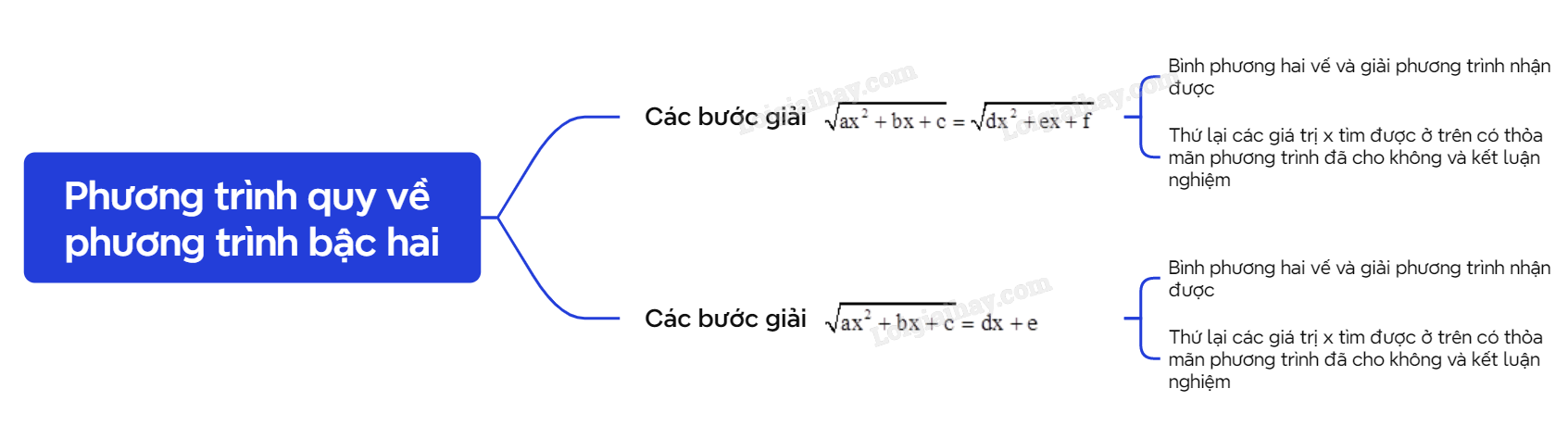
A. Lý thuyết 1. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = \sqrt {d{x^2} + ex + f} \)
2. Phương trình dạng \(\sqrt {a{x^2} + bx + c} = dx + e\)
B. Bài tập Bài 1: Giải phương trình \(\sqrt {2{x^2} - 4x - 2} = \sqrt {{x^2} - x - 2} \). Giải: Bình phương hai vế của phương trình, ta được \(2{x^2} - 4 - 2 = {x^2} - x - 2\). Sau khi thu gọn, ta được \({x^2} - 3x = 0\). Từ đó tìm được x = 0 hoặc x = 3. Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 3 thỏa mãn. Vậy nghiệm của phương trình đã cho là x = 3. Bài 2: Giải phương trình \(\sqrt {2{x^2} - 5x - 9} = x - 1\). Giải: Bình phương hai vế của phương trình, ta được \(2{x^2} - 5x - 9 = {x^2} - 2x + 1\). Sau khi thu gọn, ta được \({x^2} - 3x - 10 = 0\). Từ đó tìm được x = -2 hoặc x = 5. Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta chỉ thấy có x = 5 thỏa mãn. Vậy nghiệm của phương trình đã cho là x = 5.
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
