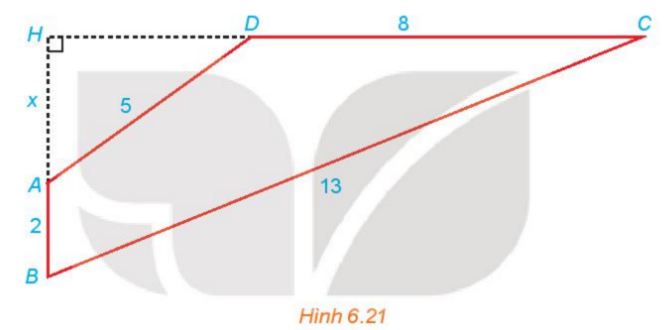
Giải bài 6.22 trang 27 SGK Toán 10 – Kết nối tri thức

Đề bài

Cho từ giác ABCD có \(AB \bot CD\); AB = 2; BC = 13; CD = 8; DA = 5 (H.6.21). Gọi H là giao điểm của AB và CD và đặt x = AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD.

Lời giải chi tiết

Ta có: AH = x (x > 0).

Xét tam giác AHD vuông ở H, ta có:

\(A{D^2} = A{H^2} + H{D^2} \)

\(\Leftrightarrow H{D^2} = A{D^2} - A{H^2} = 25 - {x^2}\)

\( \Rightarrow HD = \sqrt {25 - {x^2}} \).

Ta có: \(HC = HD + DC = \sqrt {25 - {x^2}}  + 8\),

\(HB = AH + AB = x + 2\).

Xét tam giác HBC vuông tại H, ta có:

\(B{C^2} = H{B^2} + H{C^2}\)

\(\Leftrightarrow {13^2} = {(x + 2)^2} + {\left( {\sqrt {25 - {x^2}}  + 8} \right)^2}\)

\(\Leftrightarrow 169 = {x^2} + 4x + 4 + 25 - {x^2} + 16\sqrt {25 - {x^2}}  + 64\)

\(\Leftrightarrow 16\sqrt {25 - {x^2}}  =  - 4x + 76\)

\(\Leftrightarrow 4\sqrt {25 - {x^2}}  =  - x + 19\).

Bình phương hai vế của phương trình trên ta được:

\(16(25 - {x^2}) = {x^2} - 38x + 361\)

\(\Leftrightarrow 17{x^2} - 38x - 39 = 0\)

\( \Leftrightarrow x = 3\) hoặc \(x = \frac{{ - 13}}{{17}}\).

Thay lần lượt các giá trị trên vào phương trình, ta thấy hai giá trị đều thỏa mãn.

Do x > 0 nên ta chọn x = 3. Vậy AH = 3.

\(HD = \sqrt {25 - {3^2}}  = 4\), \(HC = 4 + 8 = 12\), \(HB = 3 + 2 = 5\).

Diện tích tam giác HAD là \({S_1} = \frac{1}{2}.HA.HD = \frac{1}{2}.3.4 = 6\).

Diện tích tam giác HBC là \({S_2} = \frac{1}{2}.HB.HC = \frac{1}{2}.5.12 = 30\).

Vậy diện tích tứ giác ABCD là \(S = {S_2} - {S_1} = 30 - 6 = 24\).