Lý thuyết Hàm số y = ax² (a ≠ 0) Toán 9 Cánh diều1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\). Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Quảng cáo
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
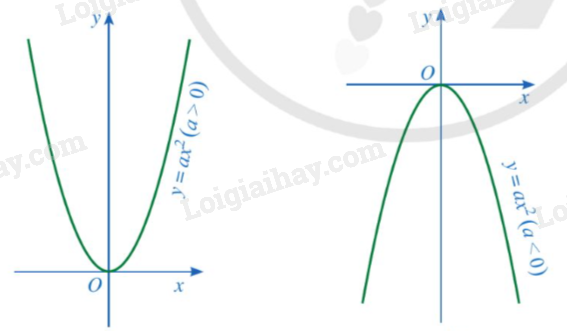
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\). 2. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\). Bảng giá trị của hàm số:
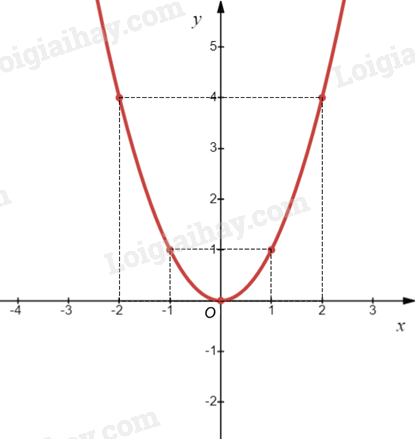
Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:
Tính chất
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
