Lý thuyết Cung và dây của một đường tròn Toán 9 Kết nối tri thức1. Dây và đường kính của đường tròn Khái niệm dây Quảng cáo
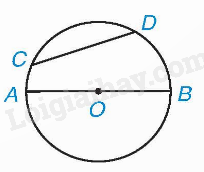
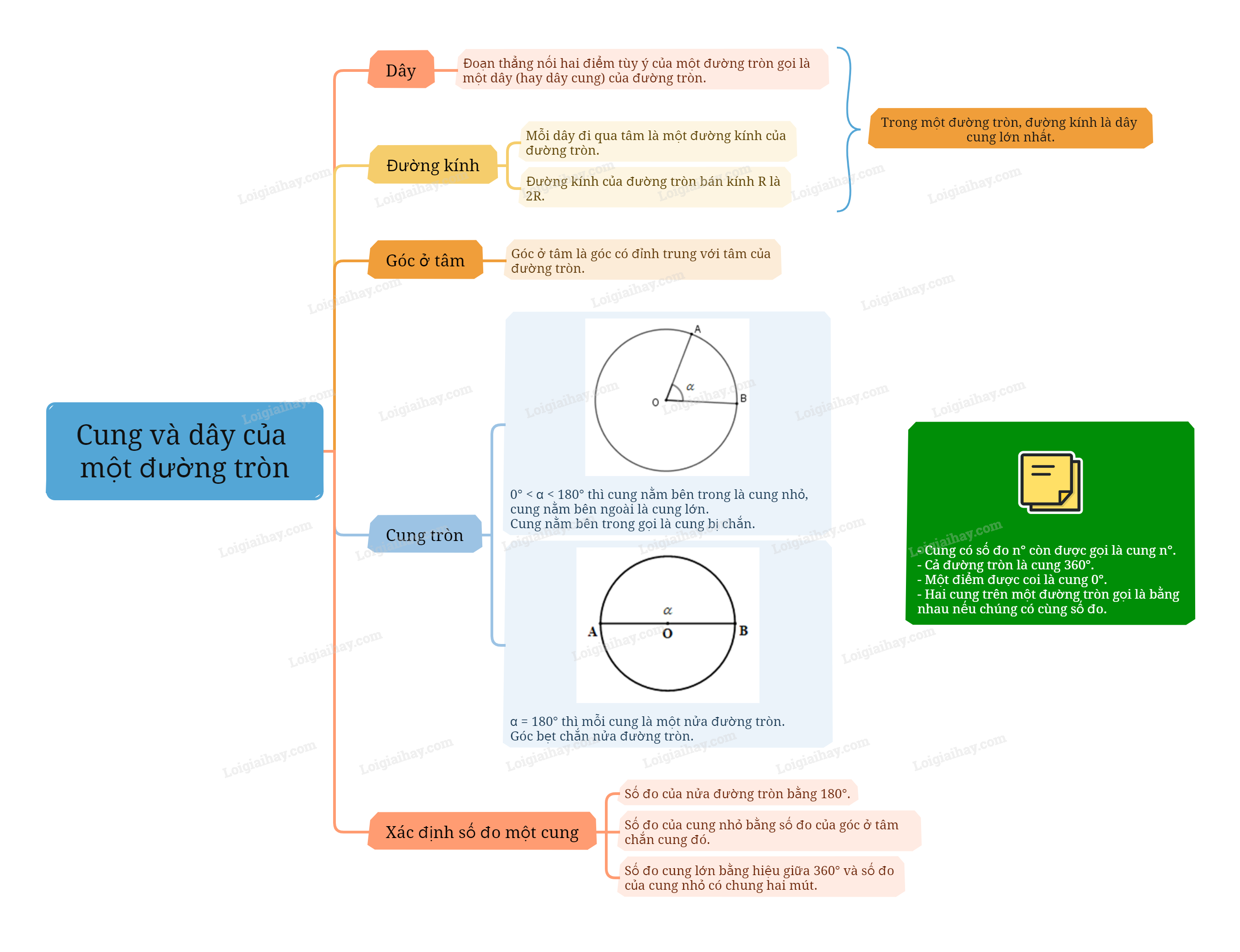
1. Dây và đường kính của đường tròn Khái niệm dây Đoạn thẳng nối hai điểm tùy ý của một đường tròn gọi là một dây (hay dây cung) của đường tròn. Khái niệm đường kính của đường tròn Mỗi dây đi qua tâm là một đường kính của đường tròn. Đường kính của đường tròn bán kính R là 2R. Ví dụ:
Trong hình trên, CD là một dây, AB là một đường kính của (O). Quan hệ giữa dây và đường kính
2. Góc ở tâm, cung và số đo của một cung Khái niệm góc ở tâm và cung tròn
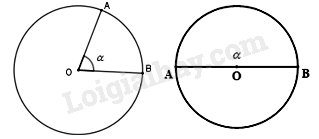
- Nếu \({0^0} < \alpha < {180^0}\) thì cung nằm bên trong góc được gọi là cung nhỏ, cung nằm bên ngoài góc được gọi là cung lớn. - Nếu \(\alpha = {180^0}\) thì mỗi cung là một nửa đường tròn. - Cung nằm bên trong gọi là cung bị chắn. Góc bẹt chắn nửa đường tròn. Ví dụ:
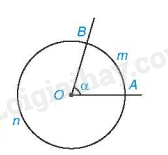
Trong hình trên, $\overset\frown{AmO}$ là cung nhỏ, ta có thể kí hiệu gọn là \(\overset\frown{AB}\). $\overset\frown{AnB}$ là cung lớn. Ta nói góc AOB chắn cung AB hay cung AB bị chắn bởi góc AOB. Cách xác định số đo một cung Số đo của một cung được xác định như sau: - Số đo của nửa đường tròn bằng \({180^0}\). - Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. - Số đo cung lớn bằng hiệu giữa \({360^0}\) và số đo của cung nhỏ có chung hai mút. Ví dụ: Số đo của cung AB được kí hiệu là sđ$\overset\frown{AB}$.
sđ$\overset\frown{AmB}=\widehat{AOB}=\alpha $; sđ$\overset\frown{AnB}={{360}^{0}}-\alpha $. Chú ý: - Cung có số đo \({n^0}\) còn được gọi là cung \({n^0}\). Cả đường tròn được coi là cung \({360^0}\). Đôi khi ta cũng coi một điểm là cung \({0^0}\). - Hai cung trên một đường tròn gọi là bằng nhau nếu chúng có cùng số đo.
|




















Danh sách bình luận