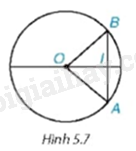
Giải mục 1 trang 87, 88 SGK Toán 9 tập 1 - Kết nối tri thứcXét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
HĐ Video hướng dẫn giải Trả lời câu hỏi Hoạt động trang 87 SGK Toán 9 Kết nối tri thức Xét dây AB tùy ý không đi qua tâm của đường tròn (O; R) (H.5.7). Dựa vào quan hệ giữa các cạnh của tam giác AOB, chứng minh AB < 2R.
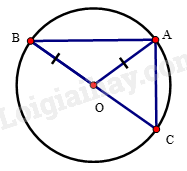
Phương pháp giải: Áp dụng bất đẳng thức tam giác đối với tam giác AOB. Lời giải chi tiết: Xét tam giác AOB có: AB < OA + OB (bất đẳng thức tam giác) mà OA = OB = R nên AB < 2R. LT1 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 1 trang 88 SGK Toán 9 Kết nối tri thức Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) trên đường tròn, ta đều có: BC < AB + AC < 2BC Phương pháp giải: - Áp dụng bất đẳng thức trong tam giác ta có: BC < AB + AC. - Theo quan hệ giữa dây và đường kính ta có: AB < BC, AC < BC Do đó: AB + AC < 2BC. Lời giải chi tiết:
Xét tam giác ABC có: BC < AB + AC (bất đẳng thức tam giác) (1) Xét đường tròn đường kính BC có dây cung AB, AC ta có: AB < BC, AC < BC Suy ra: AB + AC < 2BC (2) Từ (1) và (2) suy ra: BC < AB + AC < 2BC.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
