Lý thuyết Ba đường conic - SGK Toán 10 Kết nối tri thức1. Elip a) Định nghĩa elip Quảng cáo
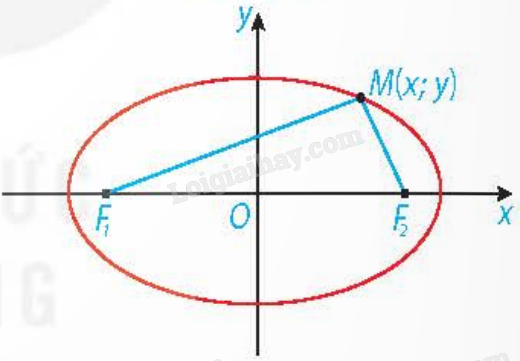
1. Elip a) Định nghĩa elip
b) Phương trình chính tắc của elip
2. Hypebol a) Định nghĩa hypebol
b) Phương trình chính tắc của hypebol
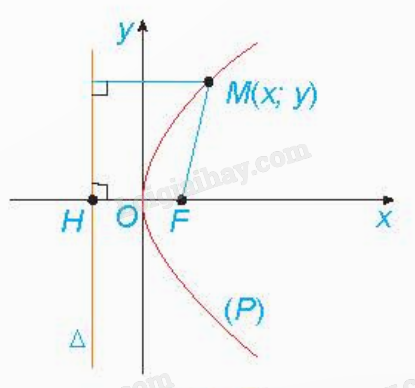
3. Parabol a) Định nghĩa parabol
b) Phương trình chính tắc của parabol
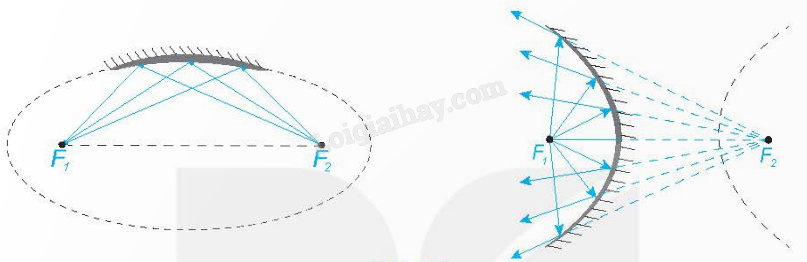
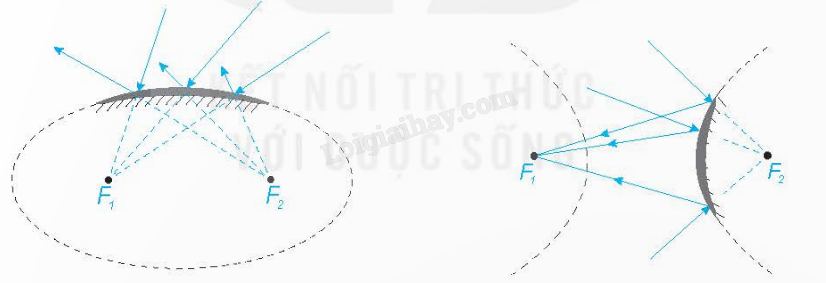
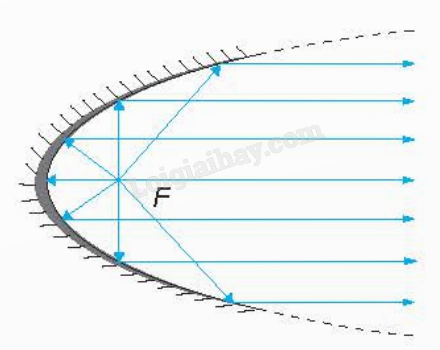
4. Một số ứng dụng của ba đường conic a) Tính chất quang học Tương tự gương cầu lồi thường đặt ở những khúc đường cua, người ta cũng có những gương (lồi, lõm) elip, hypebol, parabol. Tia sáng gặp các gương này, đều được phân xạ theo một quy tắc được xác định rõ bằng hình học.
- Tia nước bắn ra từ đài phun nước, đường đi bóng của quả bóng là những hình ảnh về đường parabol; - Khi nghiêng cốc nước hình trụ, mặt nước trong cốc có hình elip. Tương tự, dưới ánh sáng mặt trời, bóng của một quả bóng, nhìn chung, là một elip; - Ánh sáng phát ra từ một bóng đèn Led trên trần nhà có thể tạo nên trên tường các nhánh hyperbol; - Nhiều công trình kiến trúc có hình elip, parabol hay hyperbol.
B. Bài tập Bài 1: Trong các phương trình sau, phương trình nào là phương trình chính tắc của elip? a) \(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\) b) \(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = - 1\) c) \(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{4^2}}} = 1\) d) \(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\) Giải: Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với a > b > 0 nên chỉ có trường hợp d) là phương trình chính tắc của elip. Bài 2: Trong các phương trình sau, phương trình nào là phương trình chính tắc của hypebol? a) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{4^2}}} = - 1\) b) \(\frac{{{x^2}}}{{{4^2}}} - \frac{{{y^2}}}{{{5^2}}} = 1\) c) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{5^2}}} = 1\) d) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{4^2}}} = 1\) Giải: Phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a > 0, b > 0 nên các trường hợp b), c), d) là phương trình chính tắc của hypebol. Bài 3: Trong các phương trình sau, phương trình nào là phương trình chính tắc của parabol? a) \({y^2} = - 6x\) b) \({y^2} = 6x\) c) \({y^2} = - 6y\) d) \({y^2} = 6y\) Giải: Phương trình chính tắc của parabol có dạng \({y^2} = 2px\), với p > 0 nên chỉ có trường hợp d) là phương trình chính tắc của parabol. Bài 4: Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của elip. Tính tổng khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm. Giải: Ta có: \({a^2} = 25\), \({b^2} = 16\). Do đó \(c = \sqrt {{a^2} - {b^2}} = 3\). Vậy elip có hai tiêu điểm là \({F_1}( - 3;0)\), \({F_2}(3;0)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\). Ta có \(a = \sqrt {25} = 5\) nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 2a = 10. Bài 5: Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu? Giải: Ta có: \({a^2} = 9\), \({b^2} = 16\). Do đó \(c = \sqrt {{a^2} + {b^2}} = 5\). Vậy hypebol có hai tiêu điểm là \({F_1}( - 5;0)\), \({F_2}(5;0)\) và tiêu cự là \(2c = 10\). Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng \(2a = 2\sqrt 9 = 6\). Bài 6: Cho parabol (P): \({y^2} = x\). a) Tìm tiêu điểm F, đường chuẩn \(\Delta \) của (P). b) Tìm những điểm trên (P) có khoảng cách tới F bằng 3. Giải: a) Ta có \(2p = 1\) nên \(p = \frac{1}{2}\). Parabol có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\) và đường chuẩn \(\Delta :x = - \frac{1}{4}\). b) Điểm \(M({x_0};{y_0})\) thuộc (P) có khoảng cách tới F bằng 3 khi và chỉ khi \({y_0}^2 = {x_0}\) và MF = 3. Do \(MF = d(M,\Delta )\) nên \(d(M,\Delta ) = 3\). Mặt khác \(\Delta :x = - \frac{1}{4}\) và \({x_0} = {y_0}^2 \ge 0\) nên \(3 = d(M,\Delta ) = \left| {{x_0} + \frac{1}{4}} \right| = {x_0} + \frac{1}{4}\). Vậy \({x_0} = \frac{{11}}{4}\) và \({y_0} = \frac{{\sqrt {11} }}{2}\) hoặc \({y_0} = - \frac{{\sqrt {11} }}{2}\). Vậy có hai điểm M thỏa mãn bài toán với tọa độ là \(\left( {\frac{{11}}{4};\frac{{\sqrt {11} }}{2}} \right)\) và \(\left( {\frac{{11}}{4}; - \frac{{\sqrt {11} }}{2}} \right)\). Bài 7: Lập phương trình chính tắc của elip (E) có một tiêu điểm là \({F_2}(5;0)\) và đi qua điểm M(0;3). Giải: Elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0). Do \({F_2}(5;0)\) là một tiêu điểm của (E) nên c = 5. Điểm M(0;3) nằm trên (E) nên \(\frac{{{0^2}}}{{{a^2}}} + \frac{{{3^2}}}{{{b^2}}} = 1\). Do đó \({b^2} = 9\). Suy ra \({a^2} = {b^2} + {c^2} = 9 + 25 = 34\). Vậy elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{34}} + \frac{{{y^2}}}{9} = 1\). Bài 8: Lập phương trình chính tắc của hypebol (H) có một tiêu điểm là \({F_2}(6;0)\) và đi qua điểm A(4;0). Giải: Hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0). Do \({F_2}(6;0)\) là một tiêu điểm của (H) nên c = 6. Điểm A(4;0) nằm trên (H) nên \(\frac{{{4^2}}}{{{a^2}}} - \frac{{{0^2}}}{{{b^2}}} = 1\). Do đó \({a^2} = 16\). Suy ra \({b^2} = {c^2} - {a^2} = {6^2} - 16 = 20\). Vậy hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{20}} = 1\). Bài 9: Lập phương trình chính tắc của parabol (P), biết: a) (P) có tiêu điểm là F(5;0). b) (P) đi qua điểm M(2;1). Giải: Parabol (P) có phương trình chính tắc là \({y^2} = 2px\) (p > 0). a) Do F(5;0) là tiêu điểm của (P) nên \(\frac{p}{2} = 5\), tức là p = 10. Vậy parabol (P) có phương trình chính tắc là \({y^2} = 20x\). b) M(2;1) nằm trên (P) nên \({1^2} = 2p.2\), tức \(p = \frac{1}{4}\). Vậy parabol (P) có phương trình chính tắc là \({y^2} = \frac{x}{2}\).
|






















Danh sách bình luận