Giải mục 1 trang 48, 49, 50 SGK Toán 10 tập 2 - Kết nối tri thức

HĐ1

Định hai đầu của một sợi dây không đàn hồi vào hai vị trí cố định \({F_1};{F_2}\), trên một mặt bàn (độ dài sợi dây lớn hơn khoảng cách giữa hai điểm \({F_1};{F_2}\)). Kéo căng sợi dây tại một điểm M bởi một đầu bút dạ (hoặc phấn). Di chuyên đầu bút dạ để nó vẽ trên mặt bàn một đường khép kín (H7.18).

a) Đường vừa nhận được có liên hệ với hình ảnh nào ở Hình 7.17?

b) Trong quá trình đầu bút di chuyển để vẽ nên đường nói trên, tổng các khoảng cách từ nó tới các vị trí \({F_1};{F_2}\), có thay đổi không? Vì sao?

Lời giải chi tiết:

a) Đường vừa nhận được là đường “màu đỏ” trong Hình 7.17.

b) Tổng khoảng cách từ đẩu bút đến các vị trí không thay đổi

Câu hỏi

Tại sao trong định nghĩa elip cần điều kiện a > c?

Lời giải chi tiết:

Cần điều điện a>c hay 2a>2c tức là \(M{F_1} + M{F_2} > {F_1}{F_2}\), nói cách khác là để điểm M nằm ngoài đoạn \({F_1}{F_2}\), từ đó mới tạo thành elip.

Không tồn tại M để \(M{F_1} + M{F_2} < {F_1}{F_2}\) (hay a <c)

Nếu \(M{F_1} + M{F_2} = {F_1}{F_2}\) thì M thuộc đoạn \({F_1}{F_2}\), cũng không tạo thành elip.

Luyện tập 1

Trên bàn bida hình elip có một lỗ thu bị tại một tiêu điểm (H.7.20). Nếu gậy chơi tác động đủ mạnh vào một bị đặt tại tiêu điểm còn lại của bạn, thì sau khi va vào thành bàn, bị sẽ bật lại và chạy về lỗ thu (bỏ qua các tác động phụ). Hỏi độ dài quãng đường bi lăn từ điểm xuất phát tới lỗ thu có phụ thuộc vào đường đi của bị hay không? Vì sao?.

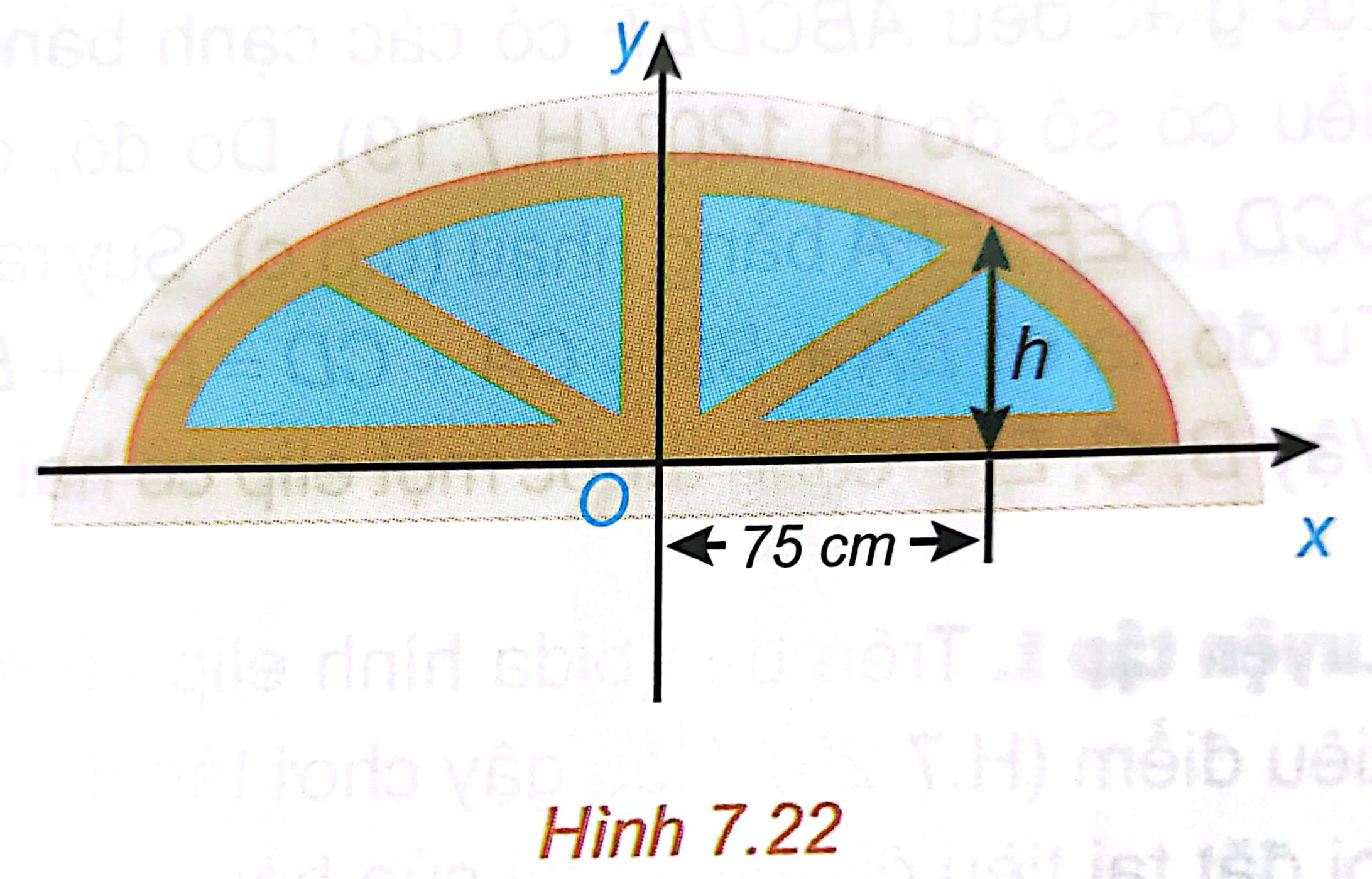
Lời giải chi tiết:

Quãng đường từ lúc bi lăn đến lúc về lỗ thu bi bằng tổng khoảng cách từ điểm bi chạm vào thành bàn tới hai tiêu điểm, dựa vào định nghĩa elip, tổng này luôn bằng 2a không đổi.

HĐ2

Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của \({F_1}{F_2}\) , tia Ox trùng tia\(O{F_2}\)(H721).

a) Nêu toạ độ của các tiêu điểm \({F_1},{F_2}\).

b) Giải thích vì sao điểm M(x;y) thuộc elip khi và chỉ khi \(\sqrt {{{\left( {x + c} \right)}^2} + {y^2}}  + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}}  = 2a\).

Lời giải chi tiết:

a)  Tọa độ 2 tiêu điểm là: \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\).

b) Ta có: \(M{F_1} = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} ,M{F_2} = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \).Vậy để điểm M thuộc Elip thì khoảng cách\(M{F_1} + M{F_2} = 2a\) nên \(\sqrt {{{\left( {x + c} \right)}^2} + {y^2}}  + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}}  = 2a\)

Luyện tập 2

Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\). Tìm các tiêu điểm và tiêu cự của elip.

Phương pháp giải:

Tìm \(c = \sqrt {{a^2} - {b^2}} \), sau đó thay vào công thức xác định hai tiêu điểm và tiêu cự

Lời giải chi tiết:

Ta có: \(c = \sqrt {{{100}^2} - {{64}^2}}  = 6\). Do đó (E) có hai tiêu điểm là \({F_1}\left( { - 6;0} \right),{F_2}\left( {6;0} \right)\) và có tiêu cự bằng 2c=12.

Vận dụng 1

Trong bản vẽ thiết kế, vòm của ô thoáng trong Hình 7.22 là nửa nằm phía trên trục hoành của elip có phương trình \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\). Biết rằng 1 đơn vị trên mặt phẳng toạ độ của bản vẽ thiết kế ứng với 30 cm trên thực tế. Tinh chiều cao h của ô thoáng tại điểm cách điểm chính giữa của đế ô thoáng 75 cm.

Lời giải chi tiết:

75 cm trên bản vẽ ứng với 2,5 đơn vị trên mặt phẳng tọa độ.

Gọi M là điểm trên vòm ô thoáng, có hoành độ 2,5 và tung độ là h.

M thuộc elip nên \(\frac{{2,{5^2}}}{{16}} + \frac{{{h^2}}}{4} = 1\)

\(\Leftrightarrow h = \sqrt {4.\left( {1 - \frac{{2,{5^2}}}{{16}}} \right)}  = \frac{{\sqrt {39} }}{4} \approx 1,56\)

Vậy độ cao h trên thực tế là: \(h = 1,56.30 = 46,8\)cm