Giải mục 2 trang 57, 58, 59 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ3

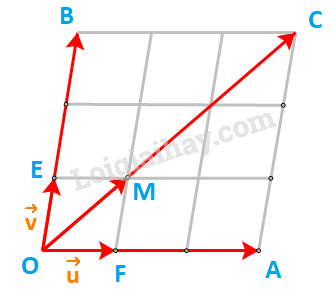
Với \(\overrightarrow u  \ne \overrightarrow 0 \) và hai số thực k, t, những khẳng định nào sau đây là đúng?

a) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) có cùng độ dài bằng \(\left| {kt} \right|.\left| {\overrightarrow u } \right|\)

b) Nếu \(kt \ge 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)

c) Nếu \(kt < 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)

d) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) bằng nhau.

Phương pháp giải:

Vecto \(k\;\overrightarrow a \) (với \(k > 0,\;\overrightarrow a  \ne \overrightarrow 0 \))  cùng hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(k\;\left| {\overrightarrow a } \right|\).

Vecto \(k\;\overrightarrow a \) (với \(k < 0,\;\overrightarrow a  \ne \overrightarrow 0 \))  ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| k \right|\;\left| {\overrightarrow a } \right|\).

Lời giải chi tiết:

a) Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) có cùng độ dài bằng \(\left| {kt} \right|.\left| {\overrightarrow u } \right|\)

Ta có: \(\left| {t\overrightarrow u } \right| = \left| t \right|\left| {\overrightarrow u } \right| \Rightarrow \left| {k\left( {t\overrightarrow u } \right)} \right| = \left| k \right|\left| {\left( {t\overrightarrow u } \right)} \right| = \left| k \right|.\left| t \right|\left| {\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)

Và \(\left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)

\( \Rightarrow \left| {k\left( {t\overrightarrow u } \right)} \right| = \left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)

b) Nếu \(kt \ge 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)

Ta xét 2 trường hợp:

Trường hợp 1: \(k \ge 0,t \ge 0\)

Vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(t\overrightarrow u \) (vì \(k \ge 0\) ), mà vecto \(t\overrightarrow u \) cùng hướng với vecto \(\overrightarrow u \) (vì \(t \ge 0\) )

Do đó vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(\overrightarrow u \).

Trường hợp 2: \(k < 0,t < 0\)

Vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(t\overrightarrow u \) (vì \(k < 0\) ), mà vecto \(t\overrightarrow u \) ngược hướng với vecto \(\overrightarrow u \) (vì \(t < 0\) )

Do đó vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(\overrightarrow u \).

Vậy vecto \(k\left( {t\overrightarrow u } \right)\) luôn cùng hướng với vecto \(\overrightarrow u \) nếu \(kt \ge 0\).

Lại có: \(kt \ge 0\) nên \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)

Vậy \(kt \ge 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) cùng hướng với \(\overrightarrow u \)

c) Nếu \(kt < 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)

Ta xét 2 trường hợp:

Trường hợp 1: \(k > 0,t < 0\)

Vecto \(k\left( {t\overrightarrow u } \right)\) cùng hướng với vecto \(t\overrightarrow u \) (vì \(k > 0\) ), mà vecto \(t\overrightarrow u \) ngược hướng với vecto \(\overrightarrow u \) (vì \(t < 0\))

Do đó vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(\overrightarrow u \).

Trường hợp 2: \(k < 0,t > 0\)

Vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(t\overrightarrow u \) (vì \(k < 0\) ), mà vecto \(t\overrightarrow u \) cùng hướng với vecto \(\overrightarrow u \) (vì \(t > 0\))

Do đó vecto \(k\left( {t\overrightarrow u } \right)\) ngược hướng với vecto \(\overrightarrow u \).

Vậy vecto \(k\left( {t\overrightarrow u } \right)\) luôn ngược hướng với vecto \(\overrightarrow u \) nếu \(kt < 0\).

Lại có: \(kt < 0\) nên \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)

Vậy \(kt < 0\) thì cả hai vecto \(k\left( {t\overrightarrow u } \right)\), \(\left( {kt} \right)\overrightarrow u \) ngược hướng với \(\overrightarrow u \)

d)

Từ ý b) và c), ra suy ra hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \)luôn cùng hướng.

Theo câu a) ta có: \(\left| {k\left( {t\overrightarrow u } \right)} \right| = \left| {\left( {kt} \right)\overrightarrow u } \right| = \left| {kt} \right|\left| {\overrightarrow u } \right|\)

\( \Rightarrow \)  Hai vecto \(k\left( {t\overrightarrow u } \right)\) và \(\left( {kt} \right)\overrightarrow u \) bằng nhau

HĐ4

Hãy chỉ ra trên Hình 4.26 hai vecto \(3\left( {\overrightarrow u  + \overrightarrow v } \right)\) và \(3\overrightarrow u  + 3\overrightarrow v \). Từ đó, nêu mối quan hệ giữa \(3\left( {\overrightarrow u  + \overrightarrow v } \right)\) và \(3\overrightarrow u  + 3\overrightarrow v \)

Lời giải chi tiết:

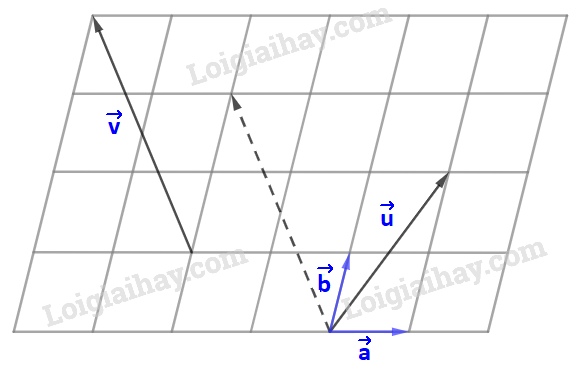
Kí hiệu O, E, F là các điểm như trên hình vẽ.

Dễ thấy: tứ giác OEMF là hình bình hành nên \(\overrightarrow {OE}  + \overrightarrow {OF}  = \overrightarrow {OM} \) hay \(\overrightarrow v  + \overrightarrow u  = \overrightarrow {OM} \)

Và \(\overrightarrow {OC}  = 3.\overrightarrow {OM}  \Rightarrow 3\left( {\overrightarrow v  + \overrightarrow u } \right) = 3.\overrightarrow {OM}  = \overrightarrow {OC} \)

Mặt khác: \(\overrightarrow {OA}  = 3.\overrightarrow {OF}  = 3\;\overrightarrow u ;\;\overrightarrow {OB}  = 3.\overrightarrow {OE}  = 3\;\overrightarrow v \)

Và \(\overrightarrow {OB}  + \overrightarrow {OA}  = \overrightarrow {OC} \) hay \(3\;\overrightarrow v  + 3\;\overrightarrow u  = \overrightarrow {OC} \)

\( \Rightarrow 3\left( {\overrightarrow v  + \overrightarrow u } \right) = 3\;\overrightarrow v  + 3\;\overrightarrow u \)

Luyện tập 2

Cho tam giác ABC có trọng tâm G. Chứng minh rằng với điểm O tùy ý, ta có

\(\overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = 3\overrightarrow {OG} \).

Phương pháp giải:

G là trọng tâm của tam giác ABC thì \(\overrightarrow {GB}  + \overrightarrow {GA}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Với 3 điểm A, B, C bất kì, ta luôn có \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

Lời giải chi tiết:

Ta có: \(\overrightarrow {OA}  = \overrightarrow {OG}  + \overrightarrow {GA} \); \(\overrightarrow {OB}  = \overrightarrow {OG}  + \overrightarrow {GB} \); \(\overrightarrow {OC}  = \overrightarrow {OG}  + \overrightarrow {GC} \)

\(\begin{array}{l} \Rightarrow \overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = \overrightarrow {OG}  + \overrightarrow {GA}  + \overrightarrow {OG}  + \overrightarrow {GB}  + \overrightarrow {OG}  + \overrightarrow {GC} \\ \Leftrightarrow \overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = 3\overrightarrow {OG}  + \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} } \right)\end{array}\)

Do G là trọng tâm của tam giác ABC nên \(\overrightarrow {GB}  + \overrightarrow {GA}  + \overrightarrow {GC}  = \overrightarrow 0 \)

\(\begin{array}{l} \Rightarrow \overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = 3\overrightarrow {OG}  + \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {OB}  + \overrightarrow {OA}  + \overrightarrow {OC}  = 3\overrightarrow {OG} \end{array}\)

Luyện tập 3

Trong hình 4.27, hãy biểu thị mỗi vecto \(\overrightarrow u ,\;\overrightarrow v \) theo hai vecto \(\overrightarrow a ,\;\overrightarrow b \), tức là tìm các số \(x,y,z,t\) để \(\overrightarrow u  = x\overrightarrow a  + y\overrightarrow b ,\;\overrightarrow v  = t\overrightarrow a  + z\overrightarrow b .\).

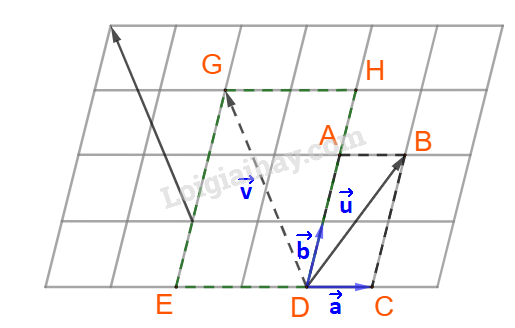
Phương pháp giải:

Phân tích vecto \(\overrightarrow u ,\;\overrightarrow v \) theo hai vecto \(\overrightarrow a ,\;\overrightarrow b \) cho trước.

Lời giải chi tiết:

Bước 1: Dựng hình bình hành có cạnh song song với giá của vecto \(\overrightarrow a ,\;\overrightarrow b \) và đường chéo là vecto \(\overrightarrow u ,\;\overrightarrow v \).

Ta dựng được hình hình hành ABCD và DEGH. Trong đó:  DC và DE nằm trên giá của vecto \(\overrightarrow a \), DA và DH nằm trên giá của vecto \(\overrightarrow b \), còn vecto \(\overrightarrow u ,\;\overrightarrow v \) lần lượt là hai dường chéo.

Dễ thấy: \(\overrightarrow u  = \overrightarrow {DA}  + \overrightarrow {DC} ,\;\overrightarrow v  = \overrightarrow {DH}  + \overrightarrow {DE} \)

Mà \(\overrightarrow {DA}  = 3\overrightarrow b ,\;\overrightarrow {DC}  = \overrightarrow a \;,\;\overrightarrow {DH}  = 3\overrightarrow b ,\;\overrightarrow {DE}  =  - 2\overrightarrow a .\)

\( \Rightarrow \overrightarrow u  = 2\overrightarrow b  + \overrightarrow a ,\;\,\overrightarrow v  = 3\overrightarrow b  - 2\overrightarrow a \)