Giải bài tập 7 trang 81 SGK Toán 9 tập 1 - Cánh diềuCho góc nhọn (alpha ). Biết rằng, tam giác (ABC) vuông tại (A) sao cho (widehat B = alpha ). a) Biểu diễn các tỉ số lượng giác của góc nhọn (alpha ) theo (AB,BC,CA). b) Chứng minh: ({sin ^2}alpha + {cos ^2}alpha = 1;tan alpha = frac{{sin alpha }}{{cos alpha }};cot alpha = frac{{cos alpha }}{{sin alpha }};tan alpha .cot alpha = 1). Từ đó, tính giá trị biểu thức: (S = {sin ^2}35^circ + {cos ^2}35^circ ;T = tan 61^circ .cot 61^circ ). Quảng cáo
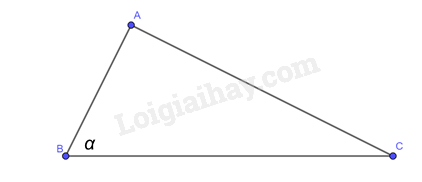
Đề bài Cho góc nhọn \(\alpha \). Biết rằng, tam giác \(ABC\) vuông tại \(A\) sao cho \(\widehat B = \alpha \). a) Biểu diễn các tỉ số lượng giác của góc nhọn \(\alpha \) theo \(AB,BC,CA\). b) Chứng minh: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\); \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\); \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\); \(\tan \alpha .\cot \alpha = 1\). Từ đó, tính giá trị biểu thức: \(S = {\sin ^2}35^\circ + {\cos ^2}35^\circ \); \(T = \tan 61^\circ .\cot 61^\circ \). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào định nghĩa tỉ số lượng giác để làm bài toán. Lời giải chi tiết
a) \(\sin \alpha = \frac{{AC}}{{BC}}\); \(\cos \alpha = \frac{{AB}}{{BC}}\); \(\tan \alpha = \frac{{AC}}{{AB}}\); \(\cot \alpha = \frac{{AB}}{{AC}}\). b) Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{BC}}} \right)^2} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1\). \(\frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{AC}}{{BC}}:\frac{{AB}}{{BC}} = \frac{{AC}}{{BC}}.\frac{{BC}}{{AB}} = \frac{{AC}}{{AB}} = \tan \alpha \). \(\frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{AB}}{{BC}}:\frac{{AC}}{{BC}} = \frac{{AB}}{{BC}}.\frac{{BC}}{{AC}} = \frac{{AB}}{{AC}} = \cot \alpha \). \(\tan \alpha .\cot \alpha = \frac{{AC}}{{AB}}.\frac{{AB}}{{AC}} = 1\). \(S = {\sin ^2}35^\circ + {\cos ^2}35^\circ = 1\). \(T = \tan 61^\circ .\cot 61^\circ = 1\).
|




















Danh sách bình luận