Giải bài tập 2 trang 100 SGK Toán 9 tập 1 - Cánh diềuXác định vị trí tương đối của hai đường tròn trong mỗi hình (17a,17b,17c,17d): Quảng cáo
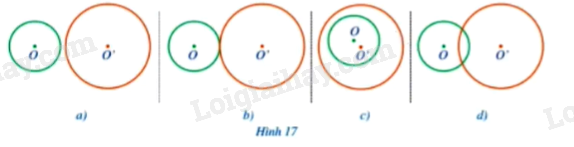
Đề bài Xác định vị trí tương đối của hai đường tròn (O) và (O') trong mỗi hình \(17a,17b,17c,17d\):
Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào kiến thức “Vị trí tương đối của hai đường tròn gồm: cắt nhau, tiếp xúc trong, tiếp xúc ngoài, ở ngoài nhau, đựng” để xác định vị trí. Lời giải chi tiết + Hình \(17a\): ở ngoài nhau. + Hình \(17b\): tiếp xúc ngoài. + Hình \(17c\): đường tròn (O') đựng đường tròn (O). + Hình \(17d\): cắt nhau.
|




















Danh sách bình luận