Bài 5.9 trang 15 SBT Vật Lí 12

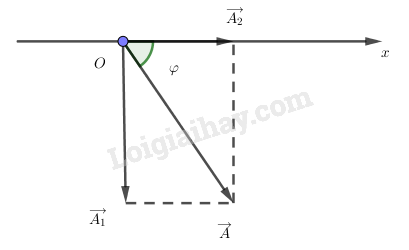
Đề bài

Hai dao động điều hòa cùng phương, cùng chu kì có phương trình lần lượt là: \({x_1} = 6\sin \dfrac{{5\pi t}}{2}(cm)\); \({x_2} = 6c{\rm{os}}\dfrac{{5\pi t}}{2}(cm)\). Tìm phương trình của dao động tổng hợp.

Lời giải chi tiết

Cách 1: Ta có: \({x_1} = 6\sin \dfrac{{5\pi t}}{2}(cm) = 6\cos (\dfrac{{5\pi t}}{2} - \dfrac{\pi }{2})(cm)\)

\(\begin{array}{l}{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \Delta \varphi\\= {6^2} + {6^2} + 2.6.6.\cos (0 + \dfrac{\pi }{2}) = 72\\ \Rightarrow A = 6\sqrt 2 cm\end{array}\)

Ta có giản đồ Fre-nen:

Ta có \(\tan \widehat {AO{A_2}} = \dfrac{{{A_1}}}{{{A_2}}} = 1\)\( \Rightarrow \widehat {AO{A_2}} = \dfrac{\pi }{4} \Rightarrow \varphi  =  - \dfrac{\pi }{4}rad\) (ở góc phần tư thứ tư)

Vậy phương trình dao động tổng hợp là: \(x = 6\sqrt 2 c{\rm{os(}}\dfrac{{5\pi t}}{2} - \dfrac{\pi }{4})(cm)\)

Cách 2:

\[{x_1} = 6\sin \frac{{5\pi t}}{2}(cm) = 6\cos (\frac{{5\pi t}}{2} - \frac{\pi }{2})(cm)\]

Phương trình tổng hợp dao động:

\[x = {x_1} + {x_2} = 6\cos (\frac{{5\pi t}}{2} - \frac{\pi }{2}) + 6\cos (\frac{{5\pi t}}{2})\]

Sử dụng máy tính ( Casio fx 570 ES)

B1: Chuyển máy tính về chế độ rad: Shift mode 4

B2: Nhập Mode 2

B3: Thực hiện phép tính: \[6\angle \frac{{ - \pi }}{2} + 6\angle 0\] shift 2 3 =

Sau khi thực hiện phép tính, máy tính hiển thị kết quả: \[6\sqrt 2 \angle \frac{{ - \pi }}{4}\]

Vậy phương trình tổng hợp có dạng: \[x = 6\sqrt 2 \cos (\frac{{5\pi }}{2}t - \frac{\pi }{4})(cm)\]

Loigiaihay.com