Giải bài 4.7 trang 54 SGK Toán 10 tập 1 – Kết nối tri thứcCho hình bình hành ABCD. Hãy tìm điểm M để BM = AB + AD. Tìm mối quan hệ giữa hai vectơ CD và CM. Quảng cáo
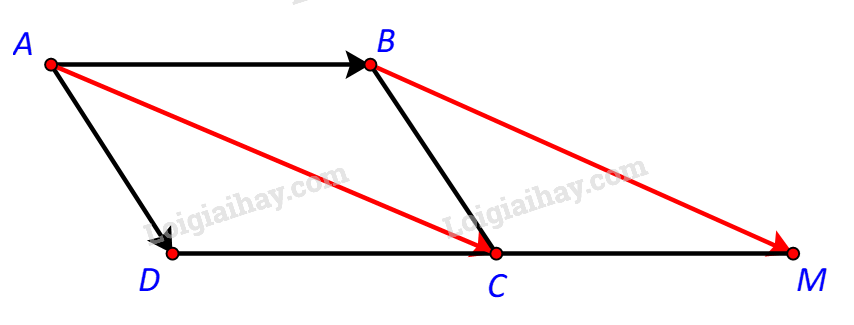
Đề bài Cho hình bình hành ABCD. Hãy tìm điểm M để \(\overrightarrow {BM} = \overrightarrow {AB} + \overrightarrow {AD} \). Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {CD} \) và \(\overrightarrow {CM} \). Phương pháp giải - Xem chi tiết Bước 1: Xác định vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) dựa vào quy tắc hình bình hành, từ đó xác định điểm M. Bước 2: Nhận xét về phương và chiều của hai vectơ \(\overrightarrow {CD} \) và \(\overrightarrow {CM} \) hoặc tìm biểu thức liên hệ giữa hai vectơ đó. Lời giải chi tiết
Ta có: \( \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) (do ABCD là hình bình hành). \( \Rightarrow \overrightarrow {BM} = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \). \( \Rightarrow \) Tứ giác ABMC là hình bình hành. \( \Rightarrow \overrightarrow {DC} =\overrightarrow {AB} = \overrightarrow {CM} \). \( \Rightarrow C\) là trung điểm DM. Vậy \(\overrightarrow {CD} = -\overrightarrow {CM} \). Chú ý khi giải +) Tứ giác ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AD} = \overrightarrow {BC} \). +) ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
|




















Danh sách bình luận