Giải bài 4.38 trang 72 SGK Toán 10 – Kết nối tri thức

Đề bài

Cho ba vectơ \(\overrightarrow a ,\;\overrightarrow b ,\;\overrightarrow u \) với \(|\overrightarrow a |\; = \;\,|\overrightarrow b |\; = 1\) và \(\overrightarrow a  \bot \overrightarrow b \). Xét một hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i  = \overrightarrow a ,\;\overrightarrow j  = \overrightarrow b .\) Chứng minh rằng:

a) Vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)

b) \(\overrightarrow u  = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a  + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \)

Lời giải chi tiết

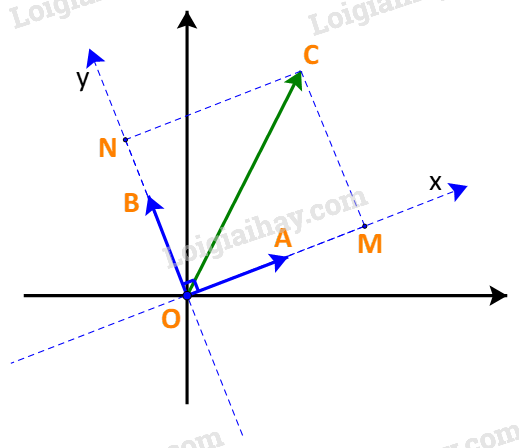
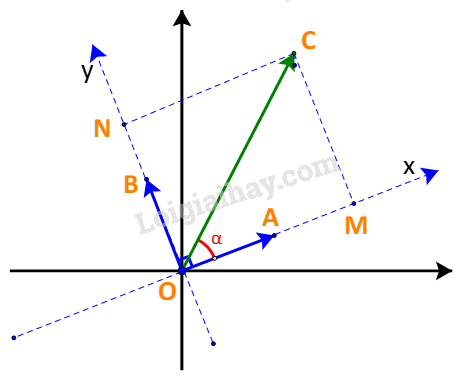
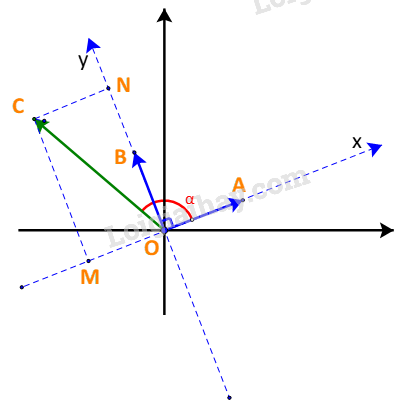
a) Trên mặt phẳng tọa độ, lấy các điểm A, B, C sao cho \(\overrightarrow {OA}  = \overrightarrow a ;\;\overrightarrow {OB}  = \overrightarrow b ;\;\overrightarrow {OC}  = \overrightarrow u \)

Trên hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i  = \overrightarrow a ,\;\overrightarrow j  = \overrightarrow b \), lấy M, N là hình chiếu của C trên Ox, Oy.

Gọi tọa độ của \(\overrightarrow u \)là \(\left( {x;y} \right)\). Đặt \(\alpha  = \left( {\overrightarrow u ,\overrightarrow a } \right)\).

+) Nếu \({0^o} < \alpha  < {90^o}\): \(x = OM = \;|\overrightarrow u |.\cos \alpha  = \;|\overrightarrow u |.\cos \alpha .\;|\overrightarrow a |\; = \overrightarrow u \,.\,\overrightarrow a \,;\)

 

+) Nếu \({90^o} < \alpha  < {180^o}\): \(x =  - OM = \; - |\overrightarrow u |.\cos ({180^o} - \alpha ) = \;|\overrightarrow u |.\cos \alpha \; = \overrightarrow u \,.\,\overrightarrow a \,;\)

 

Như vậy ta luôn có: \(x = \overrightarrow u .\overrightarrow a \)

Chứng minh tương tự, ta có: \(y = \overrightarrow u .\overrightarrow b \)

Vậy vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)

b) Trong hệ trục Oxy với các vectơ vectơ đơn vị \(\overrightarrow i  = \overrightarrow a ,\;\overrightarrow j  = \overrightarrow b \), vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)

\(\begin{array}{l} \Rightarrow \overrightarrow u  = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow i  + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow j \\ \Leftrightarrow \overrightarrow u  = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a  + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \end{array}\)