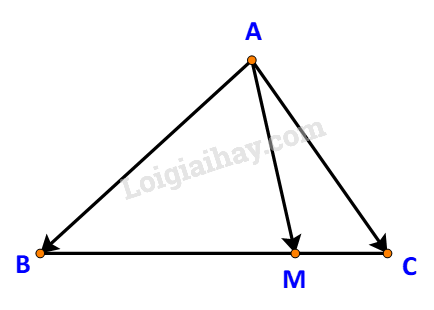
Giải bài 4.33 trang 71 SGK Toán 10 – Kết nối tri thứcTrên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3 MC. Quảng cáo
Đề bài Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3 MC. a) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) b) Biểu thị vectơ \(\overrightarrow {AM} \) theo hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Phương pháp giải - Xem chi tiết +) Nếu \(MB = k.MC\) và \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng thì \(\overrightarrow {MB} = -k.\overrightarrow {MC}\) +) \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \) (quy tắc cộng) +) \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) (quy tắc hiệu) Lời giải chi tiết
a) M thuộc cạnh BC nên vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng với nhau. Lại có: MB = 3 MC \( \Rightarrow \overrightarrow {MB} = - 3.\overrightarrow {MC} \) b) Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \) Mà \(BM = \dfrac{3}{4}BC\) nên \(\overrightarrow {BM} = \dfrac{3}{4}\overrightarrow {BC} \) \( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} \) Lại có: \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) (quy tắc hiệu) \( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \) Vậy \(\overrightarrow {AM} = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
