Đề thi giữa kì 2 Toán 8 - Đề số 7 - Kết nối tri thứcPhần trắc nghiệm (3 điểm) Câu 1: Tìm khẳng định sai:Đề bài
I. Trắc nghiệm
Câu 1 :
Tìm khẳng định sai:
Câu 2 :
Phương trình nào sau đây nhận \(x = 3\) làm nghiệm?
Câu 3 :
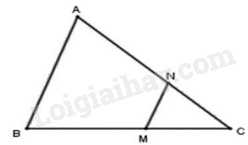
Cho tam giác \({\rm{ABC}}\) và hai điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{BC}},{\rm{AC}}\) sao cho \({\rm{MN}}\) // AB. Chọn kết luận đúng.
Câu 4 :
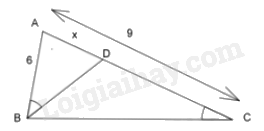
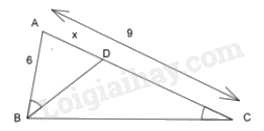
Cho hình bên biết \({\rm{AB}} = 6{\rm{\;cm}},{\rm{AC}} = 9{\rm{\;cm}},\widehat {ABD} = \widehat {BCA}\). Thế thì độ dài \({\rm{AD}}\) là:
Câu 5 :
Một ca nô xuôi dòng từ bến \(A\) đến bến \(B\) mất 4 giờ và ngược dòng từ \(B\) về \(A\) mất 5 giờ. Biết vận tốc riêng của ca nô luôn giữ không đổi là \(18{\rm{\;km}}/{\rm{h}}\). Tính vận tốc của dòng nước.
Câu 6 :
Cho hình vẽ, chỉ ra hai cặp tam giác đồng dạng.
Câu 7 :
Chọn đa thức thích hợp vào chỗ trống cho đẳng thức sau: \(\frac{{{x^3} + 8}}{{x + 2}} = \frac{ \ldots }{2}\)
Câu 8 :
Mẫu thức của phân thức \(\frac{{{x^2} - xy - x + y}}{{{x^2} + xy - x - y}}\) sau khi thu gọn có thể là:
Câu 9 :
Nghiệm của phương trình \(\frac{{x + 5}}{2} - \frac{1}{3} = \frac{{3 - 2x}}{6}\) là:
Câu 10 :
Cho \(A = \frac{{2x - 1}}{{6{x^2} - 6x}} - \frac{3}{{4{x^2} - 4}}\). Phân thức thu gọn của \(A\) có tử thức là:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Câu 1 :
Tìm khẳng định sai:
Đáp án : C Phương pháp giải :
Dựa vào tính chất của tam giác đồng dạng. Lời giải chi tiết :
Dựa vào tính chất của tam giác đồng dạng ta có:
Đáp án C.
Câu 2 :
Phương trình nào sau đây nhận \(x = 3\) làm nghiệm?
Đáp án : A Phương pháp giải :
Thay giá trị \({\rm{x}} = 3\) vào phương trình. Lời giải chi tiết :
Thay \({\rm{x}} = 3\) vào \(2{\rm{x}} - 6 = 0\) ta được \(2.3 - 6 = 0\) (luôn đúng) Vậy \(x = 3\) là nghiệm của \(2x - 6 = 0\) Đáp án A.
Câu 3 :
Cho tam giác \({\rm{ABC}}\) và hai điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{BC}},{\rm{AC}}\) sao cho \({\rm{MN}}\) // AB. Chọn kết luận đúng.
Đáp án : C Phương pháp giải :
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho. Lời giải chi tiết :
Vì \({\rm{MN}}//{\rm{AB}}\) suy ra \(\Delta CMN\) đồng dạng với \(\Delta CBA\) hay \(\Delta {\rm{NMC}}\) đồng dạng với \(\Delta {\rm{ABC}}\) Đáp án C.
Câu 4 :
Cho hình bên biết \({\rm{AB}} = 6{\rm{\;cm}},{\rm{AC}} = 9{\rm{\;cm}},\widehat {ABD} = \widehat {BCA}\). Thế thì độ dài \({\rm{AD}}\) là:
Đáp án : C Phương pháp giải :
- Từ dữ kiện đã có chứng minh được 2 tam giác đồng dạng theo trường hợp góc - góc. - Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra giá trị của . Lời giải chi tiết :
Xét \(\Delta ABD\) và \(\Delta ACB\) có: \(\widehat A\) chung \(\widehat {ABD} = \widehat {BCA}\left( {gt} \right)\) Suy ra $\Delta ABD\backsim \Delta ACB\left( g-g \right)$ Suy ra \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) \(\begin{array}{l}\frac{6}{9} = \frac{x}{6}\\x = \frac{{6.6}}{9} = 4{\rm{\;cm}}\end{array}\) Đáp án C.
Câu 5 :
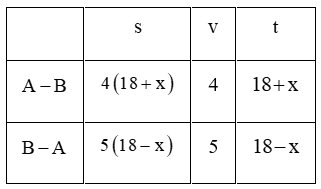
Một ca nô xuôi dòng từ bến \(A\) đến bến \(B\) mất 4 giờ và ngược dòng từ \(B\) về \(A\) mất 5 giờ. Biết vận tốc riêng của ca nô luôn giữ không đổi là \(18{\rm{\;km}}/{\rm{h}}\). Tính vận tốc của dòng nước.
Đáp án : B Phương pháp giải :
Gọi vận tốc dòng nước là \({\rm{x}}({\rm{km}}/{\rm{h}},0 < {\rm{x}} < 18)\)
Quãng đường \({\rm{AB}}\) là như nhau. Lời giải chi tiết :
Gọi vận tốc dòng nước là \({\rm{x}}({\rm{km}}/{\rm{h}},0 < {\rm{x}} < 18)\) Vận tốc ca nô xuôi dòng là: \(18 + x\left( {{\rm{\;km}}/{\rm{h}}} \right)\) Vận tốc ca nô ngược dòng là: \(18 - x\left( {{\rm{\;km}}} \right)\) Ca nô xuôi dòng mất 4 giờ, ngược dòng mất 5 giờ nên ta có: \(4\left( {18 + x} \right) = 5\left( {18 - x} \right)\) \(72 + 4x = 90 - 5x\) \(9x = 18\) \(x = 2\left( {TM} \right)\) Vậy vận tốc dòng nước là \(2{\rm{\;km}}/{\rm{h}}\) Đáp án B.
Câu 6 :
Cho hình vẽ, chỉ ra hai cặp tam giác đồng dạng.
Đáp án : B Phương pháp giải :
Trường hợp đồng dạng thứ nhất: cạnh - cạnh - cạnh: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau. Lời giải chi tiết :
Xét \(\Delta ACB\) và \(\Delta A'B'C'\), ta có: \(\frac{{AC}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AB}}{{A'C'}}\) vì \(\frac{1}{{0,5}} = \frac{2}{1} = \frac{{1,5}}{{0,75}}\). Suy ra $\Delta ACB\backsim \Delta {A}'{B}'{C}'$. Xét \(\Delta DEF\) và \({\rm{\Delta }}D'F'E'\), ta có: \(\frac{{DE}}{{D'F'}} = \frac{{DF}}{{D'E'}} = \frac{{EF}}{{E'F'}}\) vì \(\frac{{0,4}}{{0,9}} = \frac{{0,8}}{{1,8}} = \frac{{0,6}}{{1,35}}\) Suy ra $\Delta DEF\backsim \Delta {D}'{F}'{E}'$. Đáp án B.
Câu 7 :
Chọn đa thức thích hợp vào chỗ trống cho đẳng thức sau: \(\frac{{{x^3} + 8}}{{x + 2}} = \frac{ \ldots }{2}\)
Đáp án : D Phương pháp giải :
Sử dụng tính chất chất hai phân thức bằng nhau: \(\frac{A}{B} = \frac{C}{D} \Rightarrow A \cdot D = B \cdot C\) Lời giải chi tiết :
\(\frac{{{x^3} + 8}}{{x + 2}} = \frac{ \ldots }{2} \Rightarrow \ldots = \frac{{\left( {{x^3} + 8} \right) \cdot 2}}{{x + 2}} = \frac{{\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right) \cdot 2}}{{x + 2}} = 2{x^2} - 4x + 8\) Đáp án D.
Câu 8 :
Mẫu thức của phân thức \(\frac{{{x^2} - xy - x + y}}{{{x^2} + xy - x - y}}\) sau khi thu gọn có thể là:
Đáp án : C Phương pháp giải :
Rút gọn phân thức để tìm mẫu thức sau khi thu gọn. Lời giải chi tiết :
\(\frac{{{x^2} - xy - x + y}}{{{x^2} + xy - x - y}} = \frac{{x\left( {x - y} \right) - \left( {x - y} \right)}}{{x\left( {x + y} \right) - \left( {x + y} \right)}} = \frac{{\left( {x - 1} \right)\left( {x - y} \right)}}{{\left( {x - 1} \right)\left( {x + y} \right)}} = \frac{{x - y}}{{x + y}}\) Đáp án C.
Câu 9 :
Nghiệm của phương trình \(\frac{{x + 5}}{2} - \frac{1}{3} = \frac{{3 - 2x}}{6}\) là:
Đáp án : A Phương pháp giải :
- Chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó (Quy tắc chuyển vế); - Nhân cả hai vế với cùng một số khác 0 (Quy tắc nhân với một số); - Chia hai vế cho cùng một số khác 0 (Quy tắc chia cho một số). Lời giải chi tiết :
\(\frac{{x + 5}}{2} - \frac{1}{3} = \frac{{3 - 2x}}{6}\) \(\frac{{3\left( {x + 5} \right)}}{{2.3}} - \frac{{1.2}}{{3.2}} = \frac{{3 - 2x}}{6}\) \(3x + 15 - 2 = 3 - 2x\) \(3x + 2x = 3 - 15 + 2\) \(5x = - 10\) \(x = - 2\) Đáp án A.
Câu 10 :
Cho \(A = \frac{{2x - 1}}{{6{x^2} - 6x}} - \frac{3}{{4{x^2} - 4}}\). Phân thức thu gọn của \(A\) có tử thức là:
Đáp án : C Phương pháp giải :
Muốn trừ hai phân thức khác mẫu, ta quy đồng mẫu thức rồi trừ hai phân thức có cùng mẫu thức vừa tìm được Lời giải chi tiết :
\(A = \frac{{2x - 1}}{{6{x^2} - 6x}} - \frac{3}{{4{x^2} - 4}} = \frac{{2x - 1}}{{6x\left( {x - 1} \right)}} - \frac{3}{{4\left( {{x^2} - 1} \right)}}\) \( = \frac{{2x - 1}}{{6x\left( {x - 1} \right)}} - \frac{3}{{4\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{2\left( {2x - 1} \right)\left( {x + 1} \right) - 3.3x}}{{12x\left( {x - 1} \right)\left( {x + 1} \right)}}\) \( = \frac{{\left( {4x - 2} \right)\left( {x + 1} \right) - 9x}}{{12x\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{4{x^2} + 4x - 2x - 2 - 9x}}{{12\left( {x - 1} \right)\left( {x + 1} \right)}}\) \( = \frac{{4{x^2} - 7x - 2}}{{12\left( {x - 1} \right)\left( {x + 1} \right)}}\) Đáp án C.
II. Tự luận
Phương pháp giải :
Thực hiện các phép toán cộng, trừ, nhân, chia phân thức. Áp dụng linh hoạt các tính chất của phép toán. Lời giải chi tiết :
a) \(\frac{{2x + 5}}{{5{x^2}{y^2}}} + \frac{8}{{5x{y^2}}} + \frac{{2x - 1}}{{{x^2}{y^2}}} = \frac{{2x + 5 + 8x + 10x - 5}}{{5{x^2}{y^2}}} = \frac{{20x}}{{5{x^2}{y^2}}} = \frac{4}{{x{y^2}}}\) \( = \frac{{4{x^2} - 3x + 5 - \left( {1 - 2x} \right)\left( {x - 1} \right) - 6\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\) \( = \frac{{4{x^2} - 3x + 5 - x + 1 + 2{x^2} - 2x - 6{x^2} - 6x - 6}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{ - 12x}}{{{x^3} - 1}}\) Phương pháp giải :
Điều kiện xác định của phân thức là mẫu thức khác 0 . Rút gọn biểu thức bằng cách thực hiện các phép toán cộng, trừ, nhân, chia phân thức. Lời giải chi tiết :
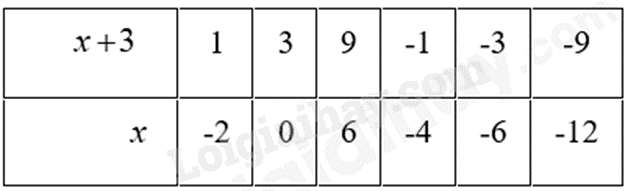
a) ĐКXĐ: \(\left\{ {\begin{array}{*{20}{l}}{x + 3 \ne 0}\\{x - 3 \ne 0}\\{{x^2} - 9 \ne 0}\\{x + 2 \ne 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne \pm 3}\\{x \ne - 2}\end{array}} \right.} \right.\) \(A = \left( {\frac{{2x - 1}}{{x + 3}} + \frac{x}{{x - 3}} - \frac{{3 - 10x}}{{{x^2} - 9}}} \right):\frac{{x + 2}}{{x - 3}}\) \(A = \frac{{\left( {2x - 1} \right)\left( {x - 3} \right) + x\left( {x + 3} \right) - \left( {3 - 10x} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\) \(A = \frac{{2{x^2} - 6x - x + 3 + {x^2} + 3x - 3 + 10x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\) \(A = \frac{{3{x^2} + 6x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\) \(A = \frac{{3x\left( {x + 2} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\) \(A = \frac{{3x}}{{x + 3}}\) Để nhận giá trị nguyên thì \(\frac{9}{{x + 3}}\) nguyên \( \Rightarrow 9:\left( {x + 3} \right) \Rightarrow x + 3 \in U\left( 9 \right)\) Ta có bảng sau:
Đối chiếu ĐKXĐ ta được \(x \in \left\{ { - 12, - 6, - 4,0,6} \right\}\) Vậy \(x \in \left\{ { - 12, - 6, - 4,0,6} \right\}\) thì \(A\) nhận giá trị nguyên. Phương pháp giải :
Bước 1. Lập phương trình. - Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết. - Lập phương trình biểu diễn mối quan hệ giữa các đại lượng. Bước 2. Giải phương trình. Bước 3. Trả lời. - Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không. - Kết luận. Lời giải chi tiết :
Gọi số học sinh lớp \(8A\) là \({\rm{x}}\) (học sinh). Điều kiện: \({\rm{x}} \in {\mathbb{N}^{\rm{*}}}\). Số học sinh giỏi lớp 8A trong học kì I là: \(\frac{{\rm{x}}}{8}\) (học sinh). Số học sinh giỏi lớp 8A trong học kì II là: \(\frac{{\rm{x}}}{8} + 3\) (học sinh). Vì số học sinh giỏi trong học kì II bằng \(20{\rm{\% }}\) số học sinh cả lớp nên ta có \({\rm{PT}}\) : \(\frac{x}{8} + 3 = 20{\rm{\% }}.x\) \(\frac{x}{8} + 3 = \frac{x}{5}\) \(\frac{x}{5} - \frac{x}{8} = 3\) \(\frac{{3x}}{{40}} = 3\) \(x = 40\left( {TM} \right)\) Vậy lớp 8A có 40 học sinh. Phương pháp giải :
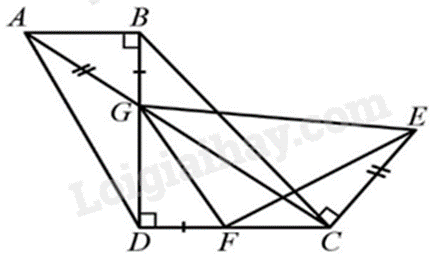
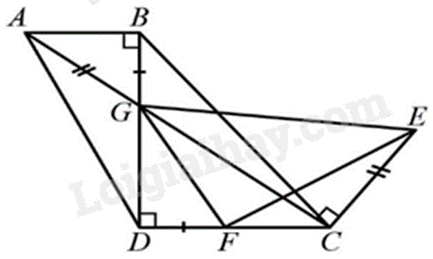
a) Sử dụng hệ quả định lí Thales, kết hợp với giả thiết suy ra cặp tương ứng tỉ lệ. Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng. b) TH đồng dạng thứ hai (c-g-c): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng. c) Suy ra góc tương ứng bằng nhau. Lời giải chi tiết :
a) Vì \(AB//CD \Rightarrow \frac{{BG}}{{AG}} = \frac{{GD}}{{GC}}\) (hệ quả định lí Thales) Mặt khác \(AG = CE,BG = DF\) nên \(\frac{{DF}}{{CE}} = \frac{{GD}}{{GC}}\). Mà \(\widehat {GDF} = \widehat {GCE} = {90^0}\) nên $\Delta FDG\backsim \Delta ECG\left( \text{dpcm} \right)$ b) Vì $\Delta FDG\backsim \Delta ECG\Rightarrow \left\{ \begin{array}{*{35}{l}} \widehat{DGF}=\widehat{CGE}\\ \frac{DG}{GF}=\frac{GC}{GE} \end{array} \right.$ \(\widehat {DGF} = \widehat {CGE}\) Suy ra \(\widehat {DGF} + \widehat {FGC} = \widehat {CGE} + \widehat {FGC}\) Suy ra \(\widehat {DGC} = \widehat {FGE}\) Từ đó, ta có $\Delta GDC\backsim \Delta GFE$ vì \(\frac{{DG}}{{GF}} = \frac{{GC}}{{GE}}\) và \(\widehat {DGC} = \widehat {FGE}\). c) Vì $\Delta GDC\backsim \Delta GFE$ nên \(\widehat {GFE} = \widehat {GDC} = {90^0}\). Phương pháp giải :
- Biến đổi các biểu thức hữu tỉ - Sử dụng tính chất của dãy tỉ số bằng nhau. Từ đó đưa bài toán ban đầu về bài toán đơn giản hơn - Thực hiện tính toán Lời giải chi tiết :
Ta có \(\frac{{x - y - z}}{x} = \frac{{y - z - x}}{y} = \frac{{z - x - y}}{z}\) \(1 - \frac{{y + z}}{x} = 1 - \frac{{z + x}}{y} = 1 - \frac{{x + y}}{z}\) \( - \frac{{y + z}}{x} = - \frac{{z + x}}{y} = - \frac{{x + y}}{z}\) \(\frac{{y + z}}{x} = \frac{{z + x}}{y} = \frac{{x + y}}{z} = \frac{{y + z + z + x + x + y}}{{x + y + z}} = 2\) \(\left\{ {\begin{array}{*{20}{l}}{y + z = 2x}\\{z + x = 2y}\\{x + y = 2z}\end{array}} \right.\) \(S = \left( {1 + \frac{y}{x}} \right)\left( {1 + \frac{z}{y}} \right)\left( {1 + \frac{x}{z}} \right) = \left( {\frac{{x + y}}{x}} \right)\left( {\frac{{y + z}}{y}} \right)\left( {\frac{{z + x}}{z}} \right) = \frac{{2z}}{x} \cdot \frac{{2x}}{y} \cdot \frac{{2y}}{z} = 8\) Vậy \(S = 8\).
|























Danh sách bình luận