Đề thi, đề kiểm tra Toán lớp 8 - Kết nối tri thức

Đề thi học kì 1 Toán 8 - Đề số 4 - Kết nối tri thức

Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên

Tải về

Tải về đề thi và đáp án Tải về đề thi Tải về đáp án
Làm đề thi

Phần trắc nghiệm (3 điểm) Câu 1: Kết quả thương của phép chia (left( 3x{{y}^{2}}-2{{x}^{2}}y+{{x}^{3}} right):left( -frac{1}{2}x right)) là :

Đề bài

I. Trắc nghiệm
Câu 1 :

Kết quả thương của phép chia \(\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\) là:

  • A
    \( - \frac{3}{2}{y^2} + xy - \frac{1}{2}{x^2}\).
  • B
    \(3{y^2} + 2xy + {x^2}\).
  • C
    \( - 6{y^2} + 4xy - 2{x^2}\).   
  • D
    \(6{y^2} - 4xy + {x^2}\).
Câu 2 :

Giá trị của đa thức \({x^3}y - 14{y^3} - 6x{y^2} + y + 2\) tại x = -1 ; y = 0,5 là:

  • A
    1.
  • B
    0,75.
  • C
    2,5.
  • D
    1,75.
Câu 3 :

Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.

a. \(\left( {x - y} \right)\left( {x + y} \right)\)

b. \(10x - 25 - {x^2}\)

c. \(8{x^3} - \frac{1}{8}\)

1. \( - {\left( {x - 5} \right)^2}\)

2. \({x^2} - {y^2}\)

3. \(\left( {2x - \frac{1}{2}} \right)\left( {4{x^2} + x + \frac{1}{4}} \right)\)

Câu 4 :

Hai đường chéo của hình chữ nhật

  • A
    song song với nhau.
  • B
    vuông góc với nhau.
  • C
    bằng nhau.
  • D
    là các đường phân giác của các góc.
Câu 5 :

Một tứ giác là hình bình hành nếu nó là:

  • A
    Tứ giác có hai cạnh song song với nhau.
  • B
    Tứ giác có hai cạnh đối bằng nhau.
  • C
    Tứ giác có hai cạnh đối song song và bằng nhau.
  • D
    Tứ giác có hai góc đối bằng nhau.
Câu 6 :

Những tứ giác nào sau đây có hai đường chéo bằng nhau?

  • A
    Hình chữ nhật, hình thang, hình vuông.
  • B
    Hình chữ nhật, hình thang cân, hình vuông.
  • C
    Hình thang cân, hình bình hành, hình chữ nhật.
  • D
    Hình thoi, hình chữ nhật, hình thang cân.
Câu 7 :

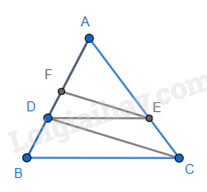
Cho tam giác ABC có AB = 9cm; \(D \in AB\) sao cho AD = 6cm. Kẻ DE // BC (\(E \in AC\)); EF // CD (\(F \in AB\)). Tính độ dài AF.

  • A
    6cm.
  • B
    5cm.
  • C
    4cm.
  • D
    7cm.
Câu 8 :

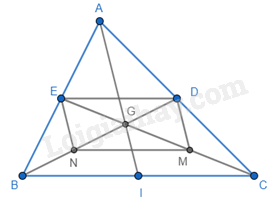
Cho tam giác ABC có ba đường trung tuyến AI, BD, CE đồng quy tại G. Gọi M và N lần lượt là trung điểm của GC và GB. Khi đó, tứ giác MNED là hình gì?

  • A
    Hình chữ nhật.
  • B
    Hình bình hành.
  • C
    Hình thang cân.
  • D
    Hình thang vuông.
Câu 9 :

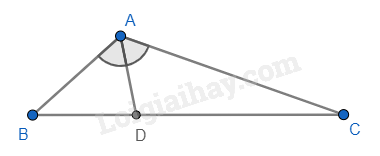
Cho tam giác ABC, AC = 2AB, AD là tia phân giác của tam giác ABC, khi đó \(\frac{{BD}}{{CD}} =?\)

  • A
    \(\frac{{BD}}{{CD}} = 1\).
  • B
    \(\frac{{BD}}{{CD}} = \frac{1}{3}\).
  • C
    \(\frac{{BD}}{{CD}} = \frac{1}{4}\).
  • D
    \(\frac{{BD}}{{CD}} = \frac{1}{2}\).
Câu 10 :

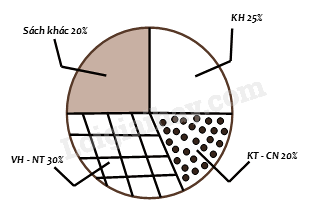
Bạn Châu vẽ biểu đồ hình quạt tròn như hình bên để biểu diễn tỉ lệ các loại sách trong thư viện: Khoa học (KH), Kĩ thuật và công nghệ (KT & CN), Văn học và Nghệ thuật (VH – NT); Sách khác. Những dữ liệu mà bạn Châu nêu ra trong biểu đồ hình quạt tròn dữ liệu nào chưa hợp lí?

  • A
    Sách khác.
  • B
    KH.
  • C
    KT - CN.
  • D
    VH - NT.

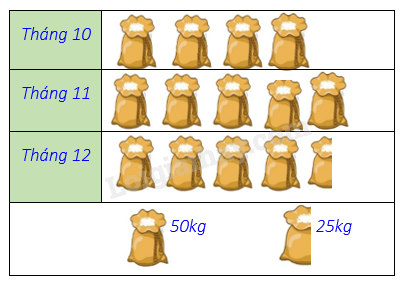
Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối  năm 2020.

Câu 11

Nêu số kg gạo bán được ở tháng 12?

  • A.
    200kg.
  • B.
    250kg.
  • C.
    225kg.
  • D.
    300kg.
Câu 12

Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ tranh ở hình bên?

  • A.
    Biểu đồ hình quạt tròn.
  • B.
    Biểu đồ cột kép.
  • C.
    Biểu đồ cột.
  • D.
    A; B; C đều đúng.
Câu 13

So tháng 10 số gạo bán được của tháng 11 tăng bao nhiêu phần trăm?

  • A.
    25%.
  • B.
    20%.
  • C.
    30%.
  • D.
    35%.
II. Tự luận
Câu 1 :

Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến.

a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\)

b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\)
Câu 2 :

Tìm x biết

a) \(9{x^2} - 72x = 0\)

b) \(\left( {16 - 4x} \right)\left( {x + 3} \right) - \left( {x + 1} \right)\left( {4 - 4x} \right) = 0\)
Câu 3 :

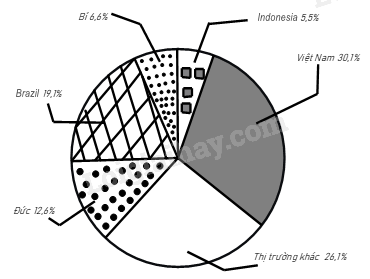
Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022.

   (Nguồn: Eurostat)

a) Trong 7 tháng đầu năm 2022 thị trường nào cung cấp cà phê cho Tây Ban Nha là nhiều nhất, ít nhất?

b) Biết lượng cà phê mà tất cả các thị trường cung cấp cho Tây Ban Nha trong 7 tháng đầu năm 2022 là 222 956 tấn. Lập bảng thống kê lượng cà phê mà các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 theo mẫu sau:

Thị trường

Đức

Braxin

Bỉ

Indonexia

Việt Nam

Khác

Lượng cà phê (tấn)

?

?

?

?

?

?
Câu 4 :

1. Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Em hãy tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?

2. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Gọi M và N theo thứ tự là trung điểm của các đoạn AH và DH.

a) Chứng minh MN//AD.

b) Gọi I là trung điểm của cạnh BC. Chứng minh tứ giác BMNI là hình bình hành.

c) Chứng minh tam giác ANI vuông tại N.
Câu 5 :

Tìm giá trị nhỏ nhất của biểu thức:\(A = 4{x^2} - 12x + 15\).

Lời giải và đáp án

I. Trắc nghiệm
Câu 1 :

Kết quả thương của phép chia \(\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\) là:

  • A
    \( - \frac{3}{2}{y^2} + xy - \frac{1}{2}{x^2}\).
  • B
    \(3{y^2} + 2xy + {x^2}\).
  • C
    \( - 6{y^2} + 4xy - 2{x^2}\).   
  • D
    \(6{y^2} - 4xy + {x^2}\).

Đáp án : C

Phương pháp giải :

Sử dụng quy tắc chia đa thức cho đơn thức.

Lời giải chi tiết :

Ta có:

\(\begin{array}{l}\left( {3x{y^2} - 2{x^2}y + {x^3}} \right):\left( { - \frac{1}{2}x} \right)\\ = 3x{y^2}:\left( { - \frac{1}{2}x} \right) - 2{x^2}y:\left( { - \frac{1}{2}x} \right) + {x^3}:\left( { - \frac{1}{2}x} \right)\\ =  - 6{y^2} + 4xy - 2{x^2}\end{array}\)

Câu 2 :

Giá trị của đa thức \({x^3}y - 14{y^3} - 6x{y^2} + y + 2\) tại x = -1 ; y = 0,5 là:

  • A
    1.
  • B
    0,75.
  • C
    2,5.
  • D
    1,75.

Đáp án : D

Phương pháp giải :

Thay x = -1 ; y = 0,5  vào biểu thức để tính giá trị.

Lời giải chi tiết :

Thay x = -1 ; y = 0,5  vào biểu thức, ta được:

\(\begin{array}{l}{( - 1)^3}.0,5 - 14{(0,5)^3} - 6( - 1){(0,5)^2} + 0,5 + 2\\ =  - 0,5 - 14.0,125 + 6.0,25 + 0,5 + 2\\ =  - 0,5 - 1,75 + 1,5 + 0,5 + 2\\ = 1,75\end{array}\)

Câu 3 :

Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.

a. \(\left( {x - y} \right)\left( {x + y} \right)\)

b. \(10x - 25 - {x^2}\)

c. \(8{x^3} - \frac{1}{8}\)

1. \( - {\left( {x - 5} \right)^2}\)

2. \({x^2} - {y^2}\)

3. \(\left( {2x - \frac{1}{2}} \right)\left( {4{x^2} + x + \frac{1}{4}} \right)\)

Đáp án

a. \(\left( {x - y} \right)\left( {x + y} \right)\)

2. \({x^2} - {y^2}\)

b. \(10x - 25 - {x^2}\)

1. \( - {\left( {x - 5} \right)^2}\)

c. \(8{x^3} - \frac{1}{8}\)

3. \(\left( {2x - \frac{1}{2}} \right)\left( {4{x^2} + x + \frac{1}{4}} \right)\)

Phương pháp giải :

Sử dụng kiến thức về các hằng đẳng thức đáng nhớ.

Lời giải chi tiết :

a. \(\left( {x - y} \right)\left( {x + y} \right) = {x^2} - {y^2} \Rightarrow \) a – 2.

b. \(10x - 25 - {x^2} = - {x^2} + 10x - 25 = - \left( {{x^2} - 10x + 25} \right) =  - {\left( {x - 5} \right)^2} \Rightarrow \) b – 1.

c. \(8{x^3} - \frac{1}{8} = \left( {2x - \frac{1}{2}} \right)\left( {4{x^2} + x + \frac{1}{4}} \right) \Rightarrow \) c – 3.

Đáp án: a – 2; b – 1; c – 3.

Câu 4 :

Hai đường chéo của hình chữ nhật

  • A
    song song với nhau.
  • B
    vuông góc với nhau.
  • C
    bằng nhau.
  • D
    là các đường phân giác của các góc.

Đáp án : C

Phương pháp giải :

Sử dụng tính chất của hình chữ nhật.

Lời giải chi tiết :

Hai đường chéo của hình chữ nhật bằng nhau nên chọn đáp án C.

Câu 5 :

Một tứ giác là hình bình hành nếu nó là:

  • A
    Tứ giác có hai cạnh song song với nhau.
  • B
    Tứ giác có hai cạnh đối bằng nhau.
  • C
    Tứ giác có hai cạnh đối song song và bằng nhau.
  • D
    Tứ giác có hai góc đối bằng nhau.

Đáp án : C

Phương pháp giải :

Dựa vào kiến thức về hình bình hành.

Lời giải chi tiết :

Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành nên chọn đáp án C.

Câu 6 :

Những tứ giác nào sau đây có hai đường chéo bằng nhau?

  • A
    Hình chữ nhật, hình thang, hình vuông.
  • B
    Hình chữ nhật, hình thang cân, hình vuông.
  • C
    Hình thang cân, hình bình hành, hình chữ nhật.
  • D
    Hình thoi, hình chữ nhật, hình thang cân.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về các hình đã học.

Lời giải chi tiết :

Những tứ giác có hai đường chéo bằng nhau là: hình thang cân, hình chữ nhật, hình vuông nên chọn đáp án B.

Câu 7 :

Cho tam giác ABC có AB = 9cm; \(D \in AB\) sao cho AD = 6cm. Kẻ DE // BC (\(E \in AC\)); EF // CD (\(F \in AB\)). Tính độ dài AF.

  • A
    6cm.
  • B
    5cm.
  • C
    4cm.
  • D
    7cm.

Đáp án : C

Phương pháp giải :

Sử dụng định lí Thales để chứng minh.

Lời giải chi tiết :

Ta có: DE // BC nên \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{6}{9} = \frac{2}{3}\) (định lí Thales)

EF // CD nên \(\frac{{AF}}{{AD}} = \frac{{AE}}{{AC}} = \frac{2}{3}\) (định lí Thales)

\( \Rightarrow AF = \frac{2}{3}AD = \frac{2}{3}.6 = 4(cm)\).

Câu 8 :

Cho tam giác ABC có ba đường trung tuyến AI, BD, CE đồng quy tại G. Gọi M và N lần lượt là trung điểm của GC và GB. Khi đó, tứ giác MNED là hình gì?

  • A
    Hình chữ nhật.
  • B
    Hình bình hành.
  • C
    Hình thang cân.
  • D
    Hình thang vuông.

Đáp án : B

Phương pháp giải :

Sử dụng tính chất đường trung bình.

Lời giải chi tiết :

Ta có BD và CE là đường trung tuyến của tam giác ABC nên D là trung điểm của AC; E là trung điểm của AB, khi đó DE là đường trung bình của tam giác ABC nên DE // BC và DE = \(\frac{1}{2}\)BC. (1)

M và N lần lượt là trung điểm của GC và GB nên MN là đường trung bình của tam giác GBC nên MN // BC và MN = \(\frac{1}{2}\)BC. (2)

Từ (1) và (2) suy ra DE // MN và DE = MN => MNED là hình bình hành (hai cạnh đối song song và bằng nhau).

Câu 9 :

Cho tam giác ABC, AC = 2AB, AD là tia phân giác của tam giác ABC, khi đó \(\frac{{BD}}{{CD}} =?\)

  • A
    \(\frac{{BD}}{{CD}} = 1\).
  • B
    \(\frac{{BD}}{{CD}} = \frac{1}{3}\).
  • C
    \(\frac{{BD}}{{CD}} = \frac{1}{4}\).
  • D
    \(\frac{{BD}}{{CD}} = \frac{1}{2}\).

Đáp án : D

Phương pháp giải :

Sử dụng tính chất của đường phân giác trong tam giác.

Lời giải chi tiết :

Ta có AD là tia phân giác của tam giác ABC nên \(\frac{{BD}}{{CD}} = \frac{{AB}}{{AC}} = \frac{{AB}}{{2AB}} = \frac{1}{2}\) (tính chất của tia phân giác trong tam giác).

Câu 10 :

Bạn Châu vẽ biểu đồ hình quạt tròn như hình bên để biểu diễn tỉ lệ các loại sách trong thư viện: Khoa học (KH), Kĩ thuật và công nghệ (KT & CN), Văn học và Nghệ thuật (VH – NT); Sách khác. Những dữ liệu mà bạn Châu nêu ra trong biểu đồ hình quạt tròn dữ liệu nào chưa hợp lí?

  • A
    Sách khác.
  • B
    KH.
  • C
    KT - CN.
  • D
    VH - NT.

Đáp án : A

Phương pháp giải :

Quan sát biểu đồ để chỉ ra dữ liệu chưa hợp lí.

Lời giải chi tiết :

Trong biểu đồ trên, ta thấy tỉ lệ của sách khác (20%) bằng tỉ lệ sách KT – CN (20%) nhưng phần biểu diễn của sách khác lại bằng với phần biểu diễn của sách KN (25%). nên dữ liệu sách khác, sách KT – CN hoặc sách KH chưa hợp lý.

Vì tổng tỉ lệ các loại sách là 100%, mà tổng số phần trăm trong biểu đồ trên là 30% + 20% + 25% + 20% = 95% < 100%.

Vậy ta suy ra dữ liệu chưa hợp lí là dữ liệu sách khác. Tỉ lệ của sách khác phải là 25% bằng với tỉ lệ của sách KH.

Biểu đồ tranh ở hình bên thống kê số gạo bán của một cửa hàng trong ba tháng cuối  năm 2020.

Câu 11

Nêu số kg gạo bán được ở tháng 12?

  • A.
    200kg.
  • B.
    250kg.
  • C.
    225kg.
  • D.
    300kg.

Đáp án : C

Phương pháp giải :

Quan sát biểu đồ tranh để trả lời câu hỏi.

Lời giải chi tiết :

Số kg gạo bán được ở tháng 12 là: 50.4 + 25 = 225 (kg).

Câu 12

Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong biểu đồ tranh ở hình bên?

  • A.
    Biểu đồ hình quạt tròn.
  • B.
    Biểu đồ cột kép.
  • C.
    Biểu đồ cột.
  • D.
    A; B; C đều đúng.

Đáp án : C

Phương pháp giải :

Quan sát biểu đồ tranh để trả lời câu hỏi.

Lời giải chi tiết :

Với dự liệu trong biểu đồ tranh trên, ta có thể biểu diễn các dữ liệu thống kê bằng biểu đồ cột.

Câu 13

So tháng 10 số gạo bán được của tháng 11 tăng bao nhiêu phần trăm?

  • A.
    25%.
  • B.
    20%.
  • C.
    30%.
  • D.
    35%.

Đáp án : A

Phương pháp giải :

Quan sát biểu đồ tranh để trả lời câu hỏi.

Lời giải chi tiết :

Số gạo tháng 10 bán được là: 50.4 = 200 (kg).

Số gạo tháng 11 bán được là: 50.5 = 250 (kg).

So với tháng 10, số gạo bán được của tháng 11 tăng là: 250 – 200 = 50 (kg).

Số gạo bán được của tháng 11 tăng so với tháng 10 số phần trăm là: \(\frac{{50}}{{200}}.100 = 25(\% )\)

II. Tự luận
Câu 1 :

Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến.

a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\)

b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\)
Phương pháp giải :

Sử dụng các phép tính với đa thức để rút gọn biểu thức.

Lời giải chi tiết :

a) \(A = 2xy + \frac{1}{2}x.\left( {2x - 4y + 4} \right) - x\left( {x + 2} \right)\)

\(\begin{array}{l} = 2xy + {x^2} - 2xy + 2x - {x^2} - 2x\\ = 0\end{array}\)            

Vì A = 0 nên biểu thức A không phụ thuộc vào giá trị của biến.

b) \(B = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\)

\(\begin{array}{l} = {\left( {x + 2} \right)^2} - {\left( {x - 3} \right)^2} - 10x\\ = \left( {x + 2 - x + 3} \right)\left( {x + 2 + x - 3} \right) - 10x\\ = 5\left( {2x - 1} \right) - 10x\\ = 10x - 5 - 10x\\ =  - 5\end{array}\)

Vì B = -5 nên biểu thức B không phụ thuộc vào giá trị của biến.

Câu 2 :

Tìm x biết

a) \(9{x^2} - 72x = 0\)

b) \(\left( {16 - 4x} \right)\left( {x + 3} \right) - \left( {x + 1} \right)\left( {4 - 4x} \right) = 0\)
Phương pháp giải :

Nhóm nhân tử chung để tìm x.

Lời giải chi tiết :

a) \(9{x^2} - 72x = 0\)

\(\begin{array}{l}9x\left( {x - 8} \right) = 0\\\left[ \begin{array}{l}x = 0\\x - 8 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = 8\end{array} \right.\end{array}\)

Vậy x = 0 hoặc x = 8.

b) \(\left( {16 - 4x} \right)\left( {x + 3} \right) - \left( {x + 1} \right)\left( {4 - 4x} \right) = 0\)

\(\begin{array}{l}4\left( {4 - x} \right)\left( {x + 3} \right) - 4\left( {x + 1} \right)\left( {1 - x} \right) = 0\\(4 - x)(x + 3) - (1 - {x^2}) = 0\\4x - {x^2} + 12 - 3x - 1 + {x^2} = 0\\x + 11 = 0\\x =  - 11\end{array}\)

Vậy x = -11.

Câu 3 :

Biểu đồ hình quạt tròn biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022.

   (Nguồn: Eurostat)

a) Trong 7 tháng đầu năm 2022 thị trường nào cung cấp cà phê cho Tây Ban Nha là nhiều nhất, ít nhất?

b) Biết lượng cà phê mà tất cả các thị trường cung cấp cho Tây Ban Nha trong 7 tháng đầu năm 2022 là 222 956 tấn. Lập bảng thống kê lượng cà phê mà các thị trường cung cấp cà phê cho Tây Ban Nha trong 7 tháng đầu năm 2022 theo mẫu sau:

Thị trường

Đức

Braxin

Bỉ

Indonexia

Việt Nam

Khác

Lượng cà phê (tấn)

?

?

?

?

?

?
Phương pháp giải :

Dựa vào biểu đồ để trả lời câu hỏi.

Lời giải chi tiết :

a) Trong 7 tháng đầu năm 2022, thị trường cung cấp cà phê cho Tây Ban Nha nhiều nhất là Việt Nam với 30,1%; thị trường cung cấp ít nhất là Indonexia với 5,5%.

b) Lượng cà phê Đức cung cấp cho Tây Ban Nha là: 222 956.12,6% = 28 092,456 (tấn)

Lượng cà phê Braxin cung cấp cho Tây Ban Nha là: 222 956.19,1% = 42 584,596 (tấn)

Lượng cà phê Bỉ cung cấp cho Tây Ban Nha là: 222 956.6,6% = 14 715,096 (tấn)

Lượng cà phê Indonexia cung cấp cho Tây Ban Nha là: 222 956.5,5% = 12 262,58 (tấn)

Lượng cà phê Việt Nam cung cấp cho Tây Ban Nha là: 222 956.30,1% = 67 109,756 (tấn)

Lượng cà phê thị trường khác cung cấp cho Tây Ban Nha là: 222 956.26,1% = 58 191,516 (tấn)

Ta có bảng giá trị:

Thị trường

Đức

Braxin

Bỉ

Indonexia

Việt Nam

Khác

Lượng cà phê (tấn)

28092,456

42584,596

14715,096

12262,58

67109,756

58191,516

 

Câu 4 :

1. Để thiết kế mặt tiền cho căn nhà cấp bốn mái thái, sau khi xác định chiều dài mái PQ = 1,5m. Chú thợ nhẩm tính chiều dài mái DE biết Q là trung điểm EC, P là trung điểm của DC. Em hãy tính giúp chú thợ xem chiều dài mái DE bằng bao nhiêu (xem hình vẽ minh họa)?

2. Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Gọi M và N theo thứ tự là trung điểm của các đoạn AH và DH.

a) Chứng minh MN//AD.

b) Gọi I là trung điểm của cạnh BC. Chứng minh tứ giác BMNI là hình bình hành.

c) Chứng minh tam giác ANI vuông tại N.
Phương pháp giải :

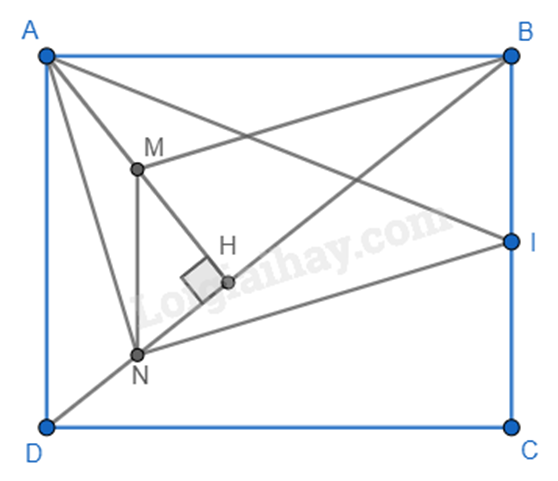
1. Dựa vào tính chất của đường trung bình để tính.

2. 

a) Dựa vào tính chất của đường trung bình để chứng minh.

b) Chứng mình BMNI có hai cạnh đối song song và bằng nhau.

c) Chứng minh M là trực tâm của tam giác ABN nên BM \( \bot \) AN, mà BM // NI nên AN \( \bot \) NI hay \(\widehat {ANI} = {90^0}\)=> ANI là tam giác vuông tại N.

Lời giải chi tiết :

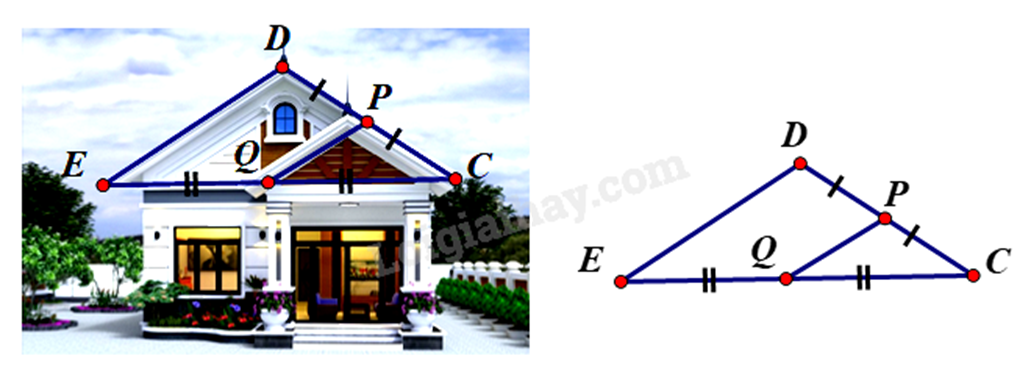
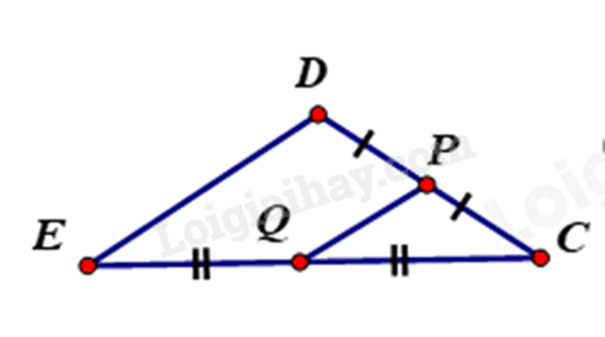
1.

Vì Q là trung điểm EC, P là trung điểm của DC nên PQ là đường trung bình của tam giác CDE.

\(\begin{array}{l} \Rightarrow QP = \frac{1}{2}DE\\ \Rightarrow DE = 2QP = 2.1,5 = 3m\end{array}\)

Vậy chiều dài mái DE bằng 3m.

2. 

a) Ta có M là trung điểm của AH, N là trung điểm của DH nên MN là đường trung bình của tam giác ADH => MN // AD và MN = \(\frac{1}{2}\)

b) Vì ABCD là hình chữ nhật nên AD // BC và AD = BC; I là trung điểm của BC nên BI = \(\frac{1}{2}\)

=> MN // BI (cùng song song với AD) và MN = BI (= \(\frac{1}{2}\)BC = \(\frac{1}{2}\)AD). Khi đó BMNI là hình bình hành.

c) Ta có MN // AD mà AD \( \bot \) AB (ABCD là hình chữ nhật) nên MN \( \bot \) Xét tam giác ABN có AH \( \bot \) BN; MN \( \bot \) AB; AH giao MN tại N nên N là trực tâm của tam giác ABN. Suy ra BM \( \bot \) AN.

Mà BM // IN (BMNI là hình bình hành) nên AN \( \bot \) IN hay \(\widehat {ANI} = {90^0}\)=> ANI là tam giác vuông tại N.

Câu 5 :

Tìm giá trị nhỏ nhất của biểu thức:\(A = 4{x^2} - 12x + 15\).
Phương pháp giải :

Biến đổi biểu thức bằng cách sử dụng hằng đẳng thức.

Lời giải chi tiết :

Ta có: \(4{x^2} - 12x + 15 = \left( {4{x^2} - 2.2x.3 + 9} \right) + 6 = {\left( {2x - 3} \right)^2} + 6\).

Vì \({\left( {2x - 3} \right)^2} \ge 0,\forall x \in \mathbb{R}\) nên \({\left( {2x - 3} \right)^2} + 6 \ge 6,\forall x \in \mathbb{R}\). Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức A.

\(\min A = 6 \Leftrightarrow 2x - 3 = 0 \Leftrightarrow x = \frac{3}{2}\).

Vậy giá trị nhỏ nhất của biểu thức A là 6 khi \(x = \frac{3}{2}\).

Bài liên quan
close