Đề thi giữa kì 2 Toán 8 - Đề số 4 - Kết nối tri thứcPhần trắc nghiệm (2 điểm) Câu 1: Phân thức bằng với phân thức (frac{x}{x-1}) là:Đề bài
I. Trắc nghiệm
Khoanh tròn trước câu trả lời đúng.
Câu 1 :
Phân thức bằng với phân thức \(\frac{x}{{x - 1}}\) là:
Câu 2 :
Phân thức nghịch đảo của phân thức \(\frac{{x - y}}{{x + y}}\) là:
Câu 3 :
Giá trị của phân thức \(\frac{{{x^2} + 4x + 4}}{{{x^2} + 2x}}\) khi \(x = - 2\) là:
Câu 4 :
Kết quả phép tính \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 4}}{{x - 1}}\) là
Câu 6 :
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AB, N là trung điểm của BC. Biết AB = 3cm, BC = 5cm. Khi đó MN bằng:
Câu 7 :
Một sân chơi có hình tam giác như hình dưới. Kích thước ba cạnh của sân lần lượt là 300m, 350m và 550m. Phía ngoài sân chơi có một con đường tạo thành một tam giác đồng dạng với sân chơi. Biết cạnh ngắn nhất của con đường là 450m. Tổng chiều dài của con đường đó là:
Câu 8 :
Cho $\Delta ABC\backsim \Delta MNP$ theo tỉ số đồng dạng 3. Gọi H, K lần lượt là trung điểm của AC, MP. Tỉ số \(\frac{{BH}}{{NK}}\) bằng
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Khoanh tròn trước câu trả lời đúng.
Câu 1 :
Phân thức bằng với phân thức \(\frac{x}{{x - 1}}\) là:
Đáp án : C Phương pháp giải :
Sử dụng tính chất của phân thức. Lời giải chi tiết :
Ta có: \(\frac{x}{{x - 1}} = \frac{{2x}}{{2\left( {x - 1} \right)}} = \frac{{2x}}{{2x - 2}}\) nên phân thức \(\frac{{2x}}{{2x - 2}} = \frac{x}{{x - 1}}\).
Câu 2 :
Phân thức nghịch đảo của phân thức \(\frac{{x - y}}{{x + y}}\) là:
Đáp án : D Phương pháp giải :
Phân thức nghịch đạo của phân thức \(\frac{A}{B}\) là \(\frac{B}{A}\). Lời giải chi tiết :
Phân thức nghịch đảo của phân thức \(\frac{{x - y}}{{x + y}}\) là \(\frac{{x + y}}{{x - y}}\).
Câu 3 :
Giá trị của phân thức \(\frac{{{x^2} + 4x + 4}}{{{x^2} + 2x}}\) khi \(x = - 2\) là:
Đáp án : D Phương pháp giải :
Kiểm tra điều kiện của phân thức, nếu thỏa mãn thì thay x = -2 vào phân thức để tính giá trị. Lời giải chi tiết :
Để phân thức \(\frac{{{x^2} + 4x + 4}}{{{x^2} + 2x}}\) xác định thì \({x^2} + 2x \ne 0 \Rightarrow \left[ \begin{array}{l}x \ne 0\\x \ne - 2\end{array} \right.\) Vì \(x = - 2\) không thỏa mãn điều kiện của phân thức nên tại \(x = - 2\) phân thức không xác định.
Câu 4 :
Kết quả phép tính \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 4}}{{x - 1}}\) là
Đáp án : A Phương pháp giải :
Sử dụng quy tắc trừ hai phân thức cùng mẫu. Lời giải chi tiết :
Ta có: \(\frac{{x + 1}}{{x - 1}} - \frac{{x - 4}}{{x - 1}} = \frac{{x + 1 - \left( {x - 4} \right)}}{{x - 1}} = \frac{{x + 1 - x + 4}}{{x - 1}} = \frac{5}{{x - 1}}\).
Đáp án : D Phương pháp giải :
Dựa vào định lí hai tam giác đồng dạng. Lời giải chi tiết :
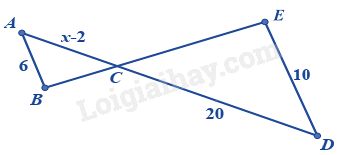
Ta có: AB // DE nên $\Delta ABC\backsim \Delta DEC$ (định lí hai tam giác đồng dạng) \(\begin{array}{l} \Rightarrow \frac{{AC}}{{CD}} = \frac{{AB}}{{DE}}\\\frac{{x - 2}}{{20}} = \frac{6}{{10}}\\ \Rightarrow x - 2 = 20.\frac{6}{{10}} = 12\\ \Rightarrow x = 12 + 2 = 14\end{array}\).
Câu 6 :
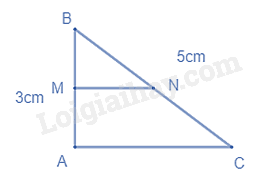
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AB, N là trung điểm của BC. Biết AB = 3cm, BC = 5cm. Khi đó MN bằng:
Đáp án : B Phương pháp giải :
Áp dụng định lí Pythagore để tính AC. Áp dụng tính chất đường trung bình trong tam giác để tính MN. Lời giải chi tiết :
Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có: \(\begin{array}{l}A{C^2} = B{C^2} - A{B^2} = {5^2} - {3^2} = 16 = {4^2}\\ \Rightarrow AC = 4\left( {cm} \right)\end{array}\) Vì M là trung điểm của AB, N là trung điểm của BC nên MN là đường trung bình của tam giác ABC \( \Rightarrow MN = \frac{1}{2}AC = \frac{1}{2}.4 = 2\left( {cm} \right)\)
Câu 7 :
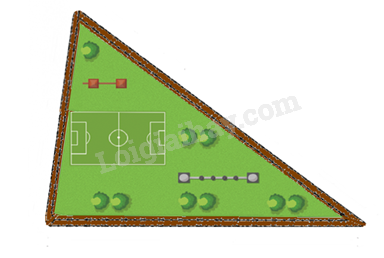
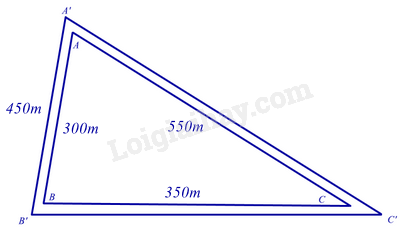
Một sân chơi có hình tam giác như hình dưới. Kích thước ba cạnh của sân lần lượt là 300m, 350m và 550m. Phía ngoài sân chơi có một con đường tạo thành một tam giác đồng dạng với sân chơi. Biết cạnh ngắn nhất của con đường là 450m. Tổng chiều dài của con đường đó là:
Đáp án : C Phương pháp giải :
Sử dụng tính chất của tam giác đồng dạng để tìm được tỉ số các cạnh của con đường. Tính tổng 3 cạnh để có chiều dài của con đường đó. Lời giải chi tiết :
Theo đề bài ta có: $\Delta ABC\backsim \Delta 'B'C'$. Do đó: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{{300}}{{450}} = \frac{2}{3}\) Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}}\\ = \frac{{300 + 350 + 550}}{{A'B' + A'C' + B'C'}} = \frac{{1200}}{{A'B' + A'C' + B'C'}} = \frac{2}{3}\\ \Rightarrow A'B' + A'C' + B'C' = 1200:\frac{2}{3} = 1800\end{array}\) Vậy chiều dài của con đường là 1800m.
Câu 8 :
Cho $\Delta ABC\backsim \Delta MNP$ theo tỉ số đồng dạng 3. Gọi H, K lần lượt là trung điểm của AC, MP. Tỉ số \(\frac{{BH}}{{NK}}\) bằng
Đáp án : C Phương pháp giải :
Sử dụng kiến thức về tỉ số hai đường trung tuyến trong hai tam giác đồng dạng. Lời giải chi tiết :
Vì H, K lần lượt là trung điểm của AC, MP nên BH và NK là hai đường trung tuyến của \(\Delta ABC\) và \(\Delta MNP\). Do B và N là hai đỉnh tương ứng trong hai tam giác đồng dạng nên BH và NK cũng là hai đường trung tuyến tương ứng \( \Rightarrow \frac{{BH}}{{NK}} = 3\).
II. Tự luận
Phương pháp giải :
Sử dụng các quy tắc tính với phân thức để thực hiện phép tính. Lời giải chi tiết :
a) \(\frac{1}{{x + 1}} + \frac{2}{{1 - x}} + \frac{{5x - 1}}{{{x^2} - 1}}\) (ĐK: \(x \ne \pm 1\)) \( = \frac{1}{{x + 1}} - \frac{2}{{x - 1}} + \frac{{5x - 1}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\) \(\begin{array}{l} = \frac{{x - 1}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} - \frac{{2\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} + \frac{{5x - 1}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\\ = \frac{{x - 1 - 2\left( {x + 1} \right) + 5x - 1}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\\ = \frac{{x - 1 - 2x - 2 + 5x - 1}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\\ = \frac{{4x - 4}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\\ = \frac{{4\left( {x - 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\\ = \frac{4}{{x + 1}}\end{array}\) b) \(\frac{{2x + 6}}{{{x^3} - 8}}:\frac{{{{\left( {x + 3} \right)}^3}}}{{2x - 4}}\) (ĐK: \(x \ne 2\)) \(\begin{array}{l} = \frac{{2\left( {x + 3} \right)}}{{\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)}}:\frac{{{{\left( {x + 3} \right)}^3}}}{{2\left( {x - 2} \right)}}\\ = \frac{{2\left( {x + 3} \right)}}{{\left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right)}}.\frac{{2\left( {x - 2} \right)}}{{{{\left( {x + 3} \right)}^3}}}\\ = \frac{4}{{\left( {{x^2} + 2x + 4} \right){{\left( {x + 3} \right)}^2}}}\end{array}\) Phương pháp giải :
a) Kiểm tra xem x = -3 có thỏa mãn điều kiện không. Nếu có thì thay x = -3 vào để tính Q. b) Sử dụng các quy tắc tính với phân thức để rút gọn P. c) Rút gọn \(P:Q\). Thay \(P:Q = \frac{5}{2}\) để tìm x. d) Để P nguyên thì tử thức phải chia hết cho mẫu thức. Lời giải chi tiết :
a) Ta có x = -3 thỏa mãn điều kiện của biểu thức Q nên thay x = -3 vào Q, ta được: \(Q = \frac{{ - 3 + 1}}{{ - 3}} = \frac{2}{3}\). Vậy \(Q = \frac{2}{3}\) khi \(x = - 3\). b) Ta có: \(P = \frac{{{x^2} - 2}}{{{x^2} + 2x}} + \frac{1}{{x + 2}}\) \(\begin{array}{l}P = \frac{{{x^2} - 2}}{{x\left( {x + 2} \right)}} + \frac{x}{{x\left( {x + 2} \right)}}\\P = \frac{{{x^2} - 2 + x}}{{x\left( {x + 2} \right)}}\\P = \frac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{x\left( {x + 2} \right)}}\\P = \frac{{x - 1}}{x}\end{array}\) Vậy \(P = \frac{{x - 1}}{x}\). c) Ta có: \(P:Q = \frac{{x - 1}}{x}:\frac{{x + 1}}{x} = \frac{{x - 1}}{x}.\frac{x}{{x + 1}} = \frac{{x - 1}}{{x + 1}}\). \(\begin{array}{l}\frac{{x - 1}}{{x + 1}} = \frac{5}{2}\\ \Rightarrow 2\left( {x - 1} \right) = 5\left( {x + 1} \right)\\2x - 2 = 5x + 5\\3x = - 7\\x = - \frac{7}{3}(TM)\end{array}\) Vậy \(x = - \frac{7}{3}\) khi \(P:Q = \frac{5}{2}\). d) Ta có: \(P = \frac{{x - 1}}{x} = 1 - \frac{1}{x}\). Để P nguyên thì \(\frac{1}{x}\) nguyên \( \Rightarrow 1 \vdots x\) hay \(x \in U\left( 1 \right) = \left\{ { - 1;1} \right\}\). Mà \(x \ne - 1\) nên chỉ có \(x = 1\) thỏa mãn. Vậy \(x = 1\) thì P nguyên. Phương pháp giải :
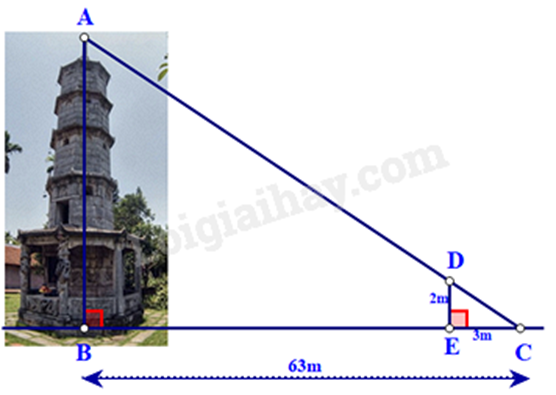
Áp dụng Định lí hai tam giác đồng dạng để chứng minh $\Delta ABC\backsim \Delta DEC$. Từ đó suy ra tỉ số các cặp cạnh tương ứng để tính chiều cao của tháp. Lời giải chi tiết :
Vì tháp và cây cột đều vuông góc với mặt đất nên ta có \(\widehat B = \widehat E = {90^0}\) \( \Rightarrow \) AB // DE $\Rightarrow \Delta ABC\backsim \Delta DEC$ (Định lí hai tam giác đồng dạng) \(\begin{array}{l} \Rightarrow \frac{{AB}}{{DE}} = \frac{{BC}}{{CE}}\\\frac{{AB}}{2} = \frac{{63}}{3} = 21\\ \Rightarrow AB = 21.2 = 42\left( m \right)\end{array}\) Vậy chiều cao của tháp là 42m. Phương pháp giải :
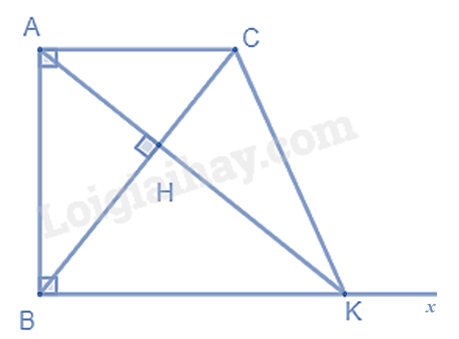
a) Chứng minh tứ giác ABKC có hai cạnh đối song song nên là hình thang và có một góc vuông nên là hình thang vuông. b) Chứng minh $\Delta ABK\backsim \Delta CHA\left( g.g \right)$ suy ra tỉ số giữa các cạnh trong hai tam giác để chứng minh $AB.AC=AK.CH$. c) Chứng minh $\Delta AHB\backsim \Delta CHA\left( g.g \right)$ để chứng minh $A{{H}^{2}}=HB.HC$. d) Áp dụng $A{{H}^{2}}=HB.HC$ để tính AH, định lí Pythagore để tính AB. Lời giải chi tiết :
a) Ta có: \(AC \bot AB\left( {gt} \right),BK \bot AB\left( {gt} \right)\) suy ra \(AC//BK\) nên tứ giác ABKC là hình thang. Mà \(\widehat A = \widehat B = {90^0}\) nên ABKC là hình thang vuông. b) Vì AC // BK nên \(\widehat {CAH} = \widehat {AKB}\) (hai góc so le trong) Xét \(\Delta ABK\) và \(\Delta CHA\) có: \(\widehat B = \widehat H\left( { = {{90}^0}} \right)\) \(\widehat {CAH} = \widehat {AKB}\) (cmt) suy ra $\Delta ABK\backsim \Delta CHA\left( g.g \right)$ (đpcm) Do đó \(\frac{{AB}}{{AK}} = \frac{{CH}}{{CA}} \) hay \(AB.CA = AK.CH\) (đpcm) c) Ta có: \(\left. \begin{array}{l}\widehat {HAC} + \widehat {ACH} = {90^0}\\\widehat {ABC} + \widehat {ACH} = {90^0}\end{array} \right\} \) nên \(\widehat {HAC} = \widehat {ABC}\) Xét \(\Delta AHB\) và \(\Delta CHA\) có: \(\widehat {AHB} = \widehat {CHA}\left( { = {{90}^0}} \right)\) \(\widehat {HAC} = \widehat {ABC}\) suy ra $\Delta AHB\backsim \Delta CHA\left( g.g \right)$ Do đó \(\frac{{AH}}{{BH}} = \frac{{CH}}{{AH}} \) hay \(A{H^2} = BH.CH\) (đpcm) d) Ta có: \(A{H^2} = BH.CH = 9.16 = 144 = {12^2}\) suy ra \(AH = 12\left( {cm} \right)\) Áp dụng định lí Pythagore vào tam giác vuông AHB, ta có: \(\begin{array}{l}A{B^2} = A{H^2} + H{B^2} = {12^2} + {9^2} = 225\\ AB = 15\left( {cm} \right)\end{array}\) Vậy AH = 12cm, AB = 15cm. Phương pháp giải :
Nhân cả tử và mẫu của phân thức \(\frac{1}{{1 + a}}\) với x; \(\frac{1}{{1 + b}}\) với y; \(\frac{1}{{1 + c}}\) với z sau đó thay \(x = by + cz\); \(y = ax + cz\); \(z = ax + by\) để biến đổi vế trái thành vế phải. Lời giải chi tiết :
Ta có: \(VT = \frac{1}{{1 + a}} + \frac{1}{{1 + b}} + \frac{1}{{1 + c}}\) \( = \frac{x}{{x\left( {1 + a} \right)}} + \frac{y}{{y\left( {1 + b} \right)}} + \frac{z}{{z\left( {1 + c} \right)}}\) \(\begin{array}{l} = \frac{x}{{x + ax}} + \frac{y}{{y + by}} + \frac{z}{{z + cz}}\\ = \frac{{by + cz}}{{by + cz + ax}} + \frac{{ax + cz}}{{ax + cz + by}} + \frac{{ax + by}}{{ax + by + cz}}\\ = \frac{{by + cz + ax + cz + ax + by}}{{ax + by + cz}}\\ = \frac{{2ax + 2by + 2cz}}{{ax + by + cz}}\\ = \frac{{2\left( {ax + by + cz} \right)}}{{ax + by + cz}}\\ = 2 = VP\end{array}\) Vậy \(\frac{1}{{1 + a}} + \frac{1}{{1 + b}} + \frac{1}{{1 + c}} = 2\) (đpcm).
|























Danh sách bình luận