Trắc nghiệm Bài 4: Hệ số góc của đường thẳng Toán 8 Chân trời sáng tạoĐề bài
Câu 1 :
: Cho hai hàm số \(y = x + 3\), \(y = mx + 3\left( {m \ne 0} \right)\) có đồ thị lần lượt là các đường thẳng \({d_1}\) và \({d_2}\). Biết rằng đường thẳng \({d_2}\) có cùng hệ số góc với đường thẳng \(y = - x + 5.\) Gọi A là giao điểm của hai đường thẳng \({d_1}\) và \({d_2}\), B là giao điểm của đường thẳng \({d_1}\) với trục Ox, C là giao điểm của đường thẳng \({d_2}\) với trục Ox. Chu vi của tam giác ABC là:
Câu 2 :
Hệ số góc của đường thẳng \(y = 2x + 1\) là:
Câu 3 :
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\).
Câu 4 :
Cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là:
Câu 5 :
Đường thẳng \(y = ax + b\) có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Câu 6 :
Chọn khẳng định đúng nhất:
Câu 8 :
Giá trị của m để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) là:
Câu 9 :
Tìm các giá trị của m để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) là:
Câu 10 :
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\left( {m \ne - 1} \right)\) trùng nhau khi:
Câu 11 :
Cho các đường thẳng sau: \(y = x + 5;y = - x + 5;y = x + 7;y = - x + 3\) Có bao nhiêu cặp 2 đường thẳng cắt nhau.
Câu 12 :
Cho hai hàm số bậc nhất \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\), có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Câu 13 :
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = 3x + 1\) và đi qua điểm \(\left( {1;7} \right)\)?
Câu 14 :
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Câu 15 :
Đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\left( {m \ne - 1} \right)\) đi qua điểm A(1; 9) có hệ số góc là:
Câu 16 :
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = - 2x - 2mx + 3.\) Với giá trị nào của m thì d cắt d’
Câu 17 :
Cho hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\). Với giá trị nào của m thì d trùng với d’?
Câu 18 :
Cho hàm số bậc nhất \(y = 2ax + a - 1\) có đồ thị hàm số là đường d. Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y - 4x + 3 = 0\) Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Câu 19 :
Hệ số góc của đường thẳng \(\frac{x}{3} + \frac{y}{2} = 1\) là:
Câu 20 :
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc \(m > 0.\) Tìm m.
Câu 21 :
Cho hàm số bậc nhất \(y = mx + 3\) có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng \(y = - x\). Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số \(y = x + 1.\) B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
Câu 22 :
Cho hàm số bậc nhất \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3\left( 1 \right)\) Tìm giá trị của m để đồ thị hàm số (1) có hệ số góc đạt giá trị nhỏ nhất.
Lời giải và đáp án
Câu 1 :
: Cho hai hàm số \(y = x + 3\), \(y = mx + 3\left( {m \ne 0} \right)\) có đồ thị lần lượt là các đường thẳng \({d_1}\) và \({d_2}\). Biết rằng đường thẳng \({d_2}\) có cùng hệ số góc với đường thẳng \(y = - x + 5.\) Gọi A là giao điểm của hai đường thẳng \({d_1}\) và \({d_2}\), B là giao điểm của đường thẳng \({d_1}\) với trục Ox, C là giao điểm của đường thẳng \({d_2}\) với trục Ox. Chu vi của tam giác ABC là:
Đáp án : C Phương pháp giải :
+ Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) + Đồ thị hàm số bậc nhất Lời giải chi tiết :
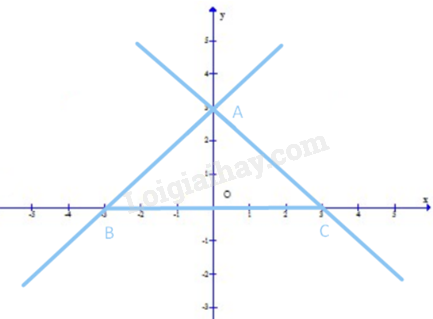
Ta có: \({d_2}:y = - x + 3\) Vẽ đồ thị của hai hàm số: \(y = x + 3\) và \(y = - x + 3\):
Từ đồ thị ta có, A(3; 0), B(-3; 0), C(3; 0) Do đó, \(OA = 3,OB = 3,OC = 3,BC = 6\) Tam giác AOB vuông tại O nên \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{3^2} + {3^2}} = \sqrt {18} \) Tam giác AOC vuông tại O nên \(AC = \sqrt {O{A^2} + O{C^2}} = \sqrt {{3^2} + {3^2}} = \sqrt {18} \) Chu vi của tam giác ABC là: \(AB + AC + BC = \sqrt {18} + \sqrt {18} + 6 = 2\sqrt {18} + 6\)
Câu 2 :
Hệ số góc của đường thẳng \(y = 2x + 1\) là:
Đáp án : B Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Hệ số góc của đường thẳng \(y = 2x + 1\) là: 2
Câu 3 :
Tìm hàm số bậc nhất có hệ số góc bằng 2 và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 1\).
Đáp án : D Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Hàm số bậc nhất có dạng \(y = ax + b\left( {a \ne 0} \right)\) Vì đường thẳng \(y = ax + b\) có hệ số góc bằng 2 nên \(a = 2\left( {tm} \right)\) Do đó hàm số: \(y = 2x + b\) Đường thẳng \(y = 2x + b\) cắt trục tung tại điểm có tung độ bằng \( - 1\) nên \(y = - 1;x = 0\) Ta có: \( - 1 = 2.0 + b\) \(b = - 1\) Do đó, hàm số cần tìm là: \(y = 2x - 1\)
Câu 4 :
Cho đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) có hệ số góc là:
Đáp án : A Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Câu 5 :
Đường thẳng \(y = ax + b\) có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là:
Đáp án : C Phương pháp giải :
Sử dụng nhận xét hệ số góc của đường thẳng: Khi hệ số góc a dương, đường thẳng \(y = ax + b\) đi lên từ trái sang phải, góc tạo bởi đường thẳng này và trục Ox là góc nhọn.
Lời giải chi tiết :
Đường thẳng \(y = ax + b\) có hệ số góc a dương thì góc tạo bởi đường thẳng này và trục Ox là góc nhọn
Câu 6 :
Chọn khẳng định đúng nhất:
Đáp án : C Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại, trùng nhau khi \(a = a',b = b'\) và ngược lại + Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại. Lời giải chi tiết :
Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại, trùng nhau khi \(a = a',b = b'\) và ngược lại Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại.
Đáp án : B Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Ta có: \(y = \frac{{3x + 1}}{3} = x + \frac{1}{3}\) nên hệ số góc của đường thẳng là 1
Câu 8 :
Giá trị của m để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) là:
Đáp án : D Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại Lời giải chi tiết :
Để đường thẳng \(y = \left( {m + 1} \right)x + 2\left( {m \ne - 1} \right)\) song song với đường thẳng \(y = - 2x + 1\) thì \(2 \ne 1\) (luôn đúng) và \(m + 1 = - 2\) \(m = - 3\) (thỏa mãn)
Câu 9 :
Tìm các giá trị của m để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) là:
Đáp án : C Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại.
Lời giải chi tiết :
Để đường thẳng \(y = \left( {m - 1} \right)x - 2\left( {m \ne 1} \right)\) cắt đường thẳng \(y = 2x\) thì \(m - 1 \ne 2\) \(m \ne 3\) (thỏa mãn)
Câu 10 :
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\left( {m \ne - 1} \right)\) trùng nhau khi:
Đáp án : C Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng trùng nhau: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) trùng nhau khi \(a = a',b = b'\) và ngược lại
Lời giải chi tiết :
Hai đường thẳng, \(y = 2mx + 1\left( {m \ne 0} \right)\) và \(y = \left( {m + 1} \right)x + 1\) trùng nhau khi: \(1 = 1\) (luôn đúng) và \(2m = m + 1\) \(m = 1\) (thỏa mãn)
Câu 11 :
Cho các đường thẳng sau: \(y = x + 5;y = - x + 5;y = x + 7;y = - x + 3\) Có bao nhiêu cặp 2 đường thẳng cắt nhau.
Đáp án : D Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại.
Lời giải chi tiết :
Các cặp 2 đường thẳng cắt nhau là: \(y = x + 5\) và \(y = - x + 5\); \(y = x + 5\) và \(y = - x + 3\); \(y = - x + 5\) và \(y = x + 7\); \(y = x + 7\) và \(y = - x + 3\) Do đó, có 4 cặp hai đường thẳng cắt nhau.
Câu 12 :
Cho hai hàm số bậc nhất \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\), có bao nhiêu giá trị của m để đồ thị của hai hàm số đã cho là hai đường thẳng song song?
Đáp án : A Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại Lời giải chi tiết :
Hàm số \(y = 2mx + 1\) là hàm số bậc nhất khi \(m \ne 0,\) hàm số \(y = \left( {m + 1} \right)x + m\) là hàm số bậc nhất khi \(m \ne - 1\) Để hai đường thẳng \(y = 2mx + 1\) và \(y = \left( {m + 1} \right)x + m\) song song với nhau thì \(\left\{ \begin{array}{l}2m = m + 1\\m \ne 1\end{array} \right. \Rightarrow \)\(\left\{ \begin{array}{l}m = 1\\m \ne 1\end{array} \right.\), do đó không có giá trị nào của m thỏa mãn bài toán.
Câu 13 :
Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng \(y = 3x + 1\) và đi qua điểm \(\left( {1;7} \right)\)?
Đáp án : C Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại
Lời giải chi tiết :
Hàm số cần tìm có dạng \(y = 3x + b\left( {b \ne 1} \right)\) Vì đường thẳng cần tìm đi qua điểm (1;7) nên ta có: \(7 = 3.1 + b,\) tìm được \(b = 4\) (thỏa mãn) Vậy hàm số cần tìm là \(y = 3x + 4\)
Câu 14 :
Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(2; 6) là:
Đáp án : C Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Gọi phương trình đường thẳng d cần tìm là \(y = ax + b\left( {a \ne 0} \right)\) Vì d đi qua gốc tọa độ nên \(b = 0 \Rightarrow y = ax\) Vì điểm M(2; 6) thuộc d nên \(6 = 2a,\) \(a = 3\) (thỏa mãn) Phương trình đường thẳng d: \(y = 3x\) nên hệ số góc của đường thẳng d là 3.
Câu 15 :
Đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\left( {m \ne - 1} \right)\) đi qua điểm A(1; 9) có hệ số góc là:
Đáp án : B Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Vì điểm A(1; 9) thuộc đường thẳng \(y = 2\left( {m + 1} \right)x + m - 2\) nên: \(9 = 2\left( {m + 1} \right).1 + m - 2\) \(3m = 9\) \(m = 3\) (thỏa mãn) Đường thẳng d: \(y = 8x + 1\), do đó đường thẳng d có hệ số góc là 8
Câu 16 :
Cho hai đồ thị hàm số bậc nhất là hai đường thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = - 2x - 2mx + 3.\) Với giá trị nào của m thì d cắt d’
Đáp án : B Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng cắt nhau: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) cắt nhau khi \(a \ne a'\) và ngược lại.
Lời giải chi tiết :
d là hàm số bậc nhất khi \(m \ne 2\) \(d':y = - 2x - 2mx + 3 = \left( { - 2 - 2m} \right)x + 3\) d’ là hàm số bậc nhất khi \(m \ne - 1\) Hai đường thẳng thẳng d: \(y = \left( {m - 2} \right)x - m\) và \(d':y = \left( { - 2 - 2m} \right)x + 3\) cắt nhau thì: \(m - 2 \ne - 2 - 2m\) \(3m \ne 0\) \(m \ne 0\) (thỏa mãn)
Câu 17 :
Cho hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\). Với giá trị nào của m thì d trùng với d’?
Đáp án : A Phương pháp giải :
Sử dụng nhận biết về hai đường thẳng trùng nhau: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) trùng nhau khi \(a = a',b = b'\) và ngược lại
Lời giải chi tiết :
d là hàm số bậc nhất khi \(m \ne - 2\) Hai đường thẳng d: \(y = \left( {m + 2} \right)x + m\) và d’: \(y = - 2x - 2m + 1\) trùng nhau khi: \(\left\{ \begin{array}{l}m + 2 = - 2\\m = - 2m + 1\end{array} \right.\; \Leftrightarrow \;\left\{ \begin{array}{l}m = - 4\\m = \frac{1}{3}\end{array} \right.\) (vô lí) Vậy không có giá trị nào của m thỏa mãn bài toán
Câu 18 :
Cho hàm số bậc nhất \(y = 2ax + a - 1\) có đồ thị hàm số là đường d. Đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y - 4x + 3 = 0\) Khi đó, điểm A(x; 6) thuộc đường thẳng d thì giá trị của x là:
Đáp án : D Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Hàm số \(y = 2ax + a - 1\) là hàm số bậc nhất khi \(a \ne 0\) d’: \(y - 4x + 3 = 0\), \(y = 4x - 3\) Vì đường thẳng d có hệ số góc gấp hai lần hệ số góc của đường thẳng d’: \(y = 4x - 3\) nên hệ số góc của đường thẳng d bằng 8, hay \(2a = 8,\) \(a = 4\) (thỏa mãn) Do đó, d: \(y = 8x + 3\) Vì điểm A(x; 6) thuộc đường thẳng d nên \(6 = 8.x + 3\) \(x = \frac{3}{8}\)
Câu 19 :
Hệ số góc của đường thẳng \(\frac{x}{3} + \frac{y}{2} = 1\) là:
Đáp án : C Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
\(\frac{x}{3} + \frac{y}{2} = 1\) \(\frac{{2x}}{3} + y = 2\) \(y = \frac{{ - 2x}}{3} + 2\) Do đó, hệ số góc của đường thẳng trên là \(\frac{{ - 2}}{3}\)
Câu 20 :
Các điểm A(m; 3) và B(1; m) nằm trên đường thẳng có hệ số góc \(m > 0.\) Tìm m.
Đáp án : D Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Đường thẳng có dạng \(y = mx + n\) (d) Vì đường thẳng d đi qua điểm A(m; 3) nên \(3 = {m^2} + n\) (1) Vì đường thẳng d đi qua điểm B(1; m) nên \(m = m + n\), tìm được \(n = 0\) Thay \(n = 0\) vào (1) ta có: \({m^2} = 3,\) tìm được \(m = \pm \sqrt 3 \) Mà \(m > 0\) nên \(m = \sqrt 3 \)
Câu 21 :
Cho hàm số bậc nhất \(y = mx + 3\) có đồ thị là đường thẳng d. Biết rằng đường thẳng d song song với đường thẳng \(y = - x\). Gọi A là giao điểm của đường thẳng d với đồ thị của hàm số \(y = x + 1.\) B là giao điểm của đường thẳng d với trục Ox. Diện tích tam giác OAB là:
Đáp án : C Phương pháp giải :
+ Sử dụng nhận biết về hai đường thẳng song song: Hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y' = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau khi \(a = a',b \ne b'\) và ngược lại + Đồ thị hàm số bậc nhất Lời giải chi tiết :
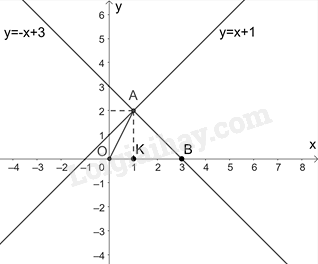
Hàm số \(y = mx + 3\) là hàm số bậc nhất khi \(m \ne 0\) Vì đường thẳng d song song với đường thẳng \(y = - x\) nên \(m = - 1\) (thỏa mãn) Do đó, d: \(y = - x + 3\) Vẽ đồ thị của hai hàm số: \(y = - x + 3\) và \(y = x + 1\):
Nhìn vào đồ thị ta thấy, A(1; 2), B(3; 0), do đó, \(OB = 3\) Gọi K là hình chiếu của A trên trục Ox, do đó AK là đường cao trong tam giác OAB và \(AK = 2\) Diện tích tam giác OAB là: \(S = \frac{1}{2}AK.OB = \frac{1}{2}.3.2 = 3\) (đvdt)
Câu 22 :
Cho hàm số bậc nhất \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3\left( 1 \right)\) Tìm giá trị của m để đồ thị hàm số (1) có hệ số góc đạt giá trị nhỏ nhất.
Đáp án : B Phương pháp giải :
Sử dụng hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
Lời giải chi tiết :
Ta có: \(y = \frac{1}{2}{m^2}x + {m^{10}} - {m^4} - \frac{1}{4}mx + 3 = \left( {\frac{1}{2}{m^2} - \frac{1}{4}m} \right)x + {m^{10}} - {m^4} + 3\) Hàm số (1) là hàm số bậc nhất khi \(\frac{1}{2}{m^2} - \frac{1}{4}m \ne 0\), tìm được \(m \ne 0,m \ne \frac{1}{2}\) Ta có: \(\frac{1}{2}{m^2} - \frac{1}{4}m = \frac{1}{2}\left( {{m^2} - \frac{1}{2}m} \right) = \frac{1}{2}\left( {{m^2} - 2.m.\frac{1}{4} + \frac{1}{{16}} - \frac{1}{{16}}} \right) = \frac{1}{2}{\left( {m - \frac{1}{4}} \right)^2} - \frac{1}{{32}} \ge \frac{{ - 1}}{{32}}\) Do đó, hệ số góc của đồ thị hàm số (1) đạt giá trị nhỏ nhất là \(\frac{{ - 1}}{{32}}\) khi \(m - \frac{1}{4} = 0\), \(m = \frac{1}{4}\) (thỏa mãn)
|



















Danh sách bình luận