Lý thuyết Tích của vecto mới một số - SGK Toán 10 Kết nối tri thức1. TÍCH CỦA VECTO VỚI MỘT SỐ 2. CÁC TÍNH CHẤT CỦA PHÉP NHÂN VECTƠ VỚI MỘT SỐ Quảng cáo
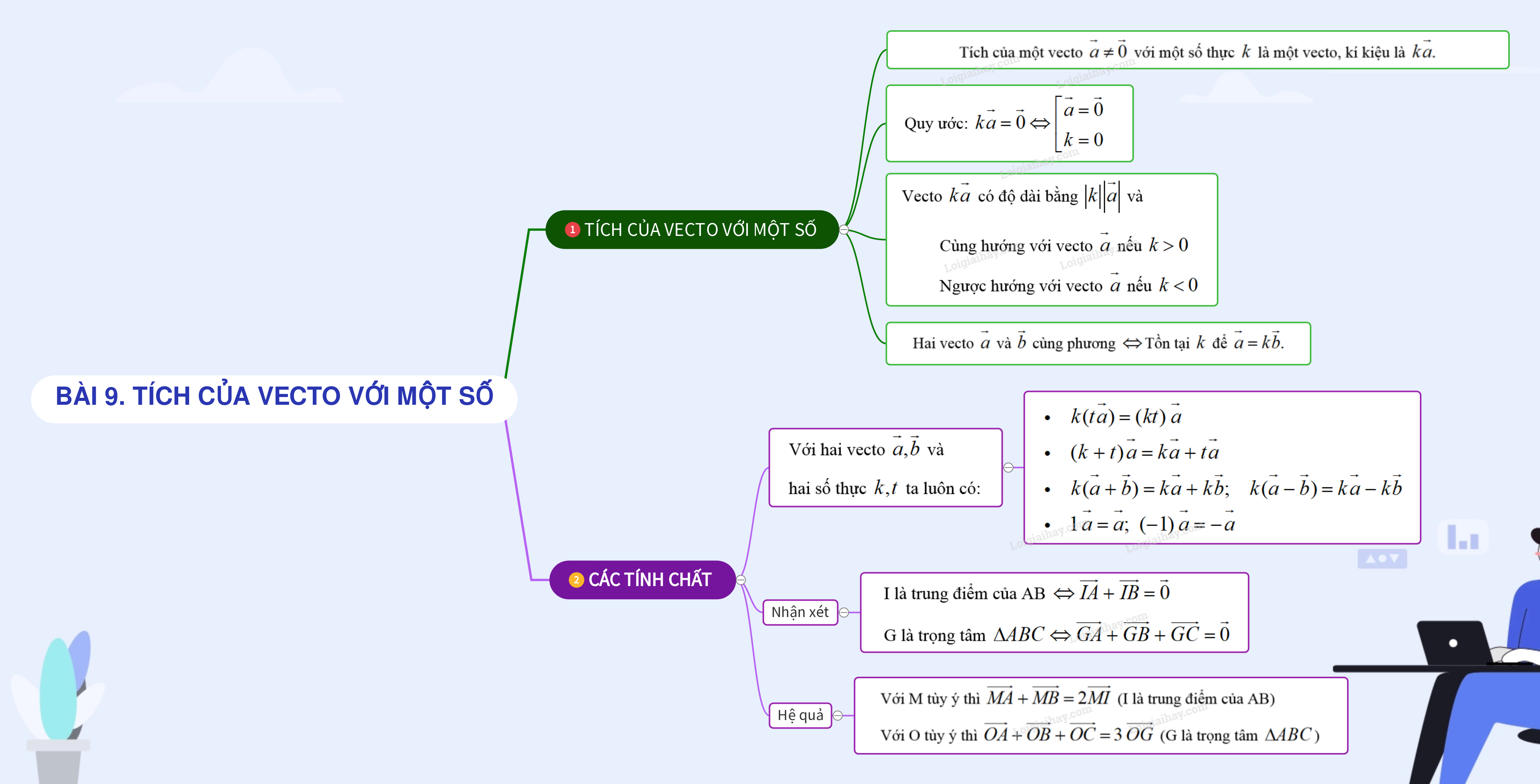
1. TÍCH CỦA VECTO VỚI MỘT SỐ +) Tích của một vecto \(\overrightarrow a \ne \overrightarrow 0 \) với một số thực \(k\) là một vecto, kí kiệu là \(k\overrightarrow a \). +) Vecto \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và Cùng hướng với vecto \(\overrightarrow a \) nếu \(k > 0\). Ngược hướng với vecto \(\overrightarrow a \) nếu \(k < 0\). +) Quy ước: \(k\overrightarrow a = \overrightarrow 0 \Leftrightarrow \left[ \begin{array}{l}\overrightarrow a = \overrightarrow 0 \\k = 0\end{array} \right.\). Nhận xét: Hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khi và chỉ khi tồn tại \(k\) để \(\overrightarrow a = k\overrightarrow b \).
2. CÁC TÍNH CHẤT CỦA PHÉP NHÂN VECTƠ VỚI MỘT SỐ +) Với hai vecto \(\overrightarrow a ,\overrightarrow b \) và hai số thực \(k,t\) ta luôn có: \(\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a = k\overrightarrow a + t\overrightarrow a \\k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b ;\quad k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a - k\overrightarrow b \\1\;\overrightarrow a = \overrightarrow a ;\;\;( - 1)\;\overrightarrow a = - \,\overrightarrow a \end{array}\) +) Nhận xét: I là trung điểm của AB \( \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \). G là trọng tâm \(\Delta ABC \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \). +) Hệ quả Với M tùy ý thì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) (I là trung điểm của AB). Với O tùy ý thì \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\;\overrightarrow {OG} \) (G là trọng tâm \(\Delta ABC\)).
|