Lý thuyết Tần số tương đối Toán 9 Cùng khám phá

1. Tần số tương đối và bảng tần số tương đối, biểu đồ tần số tương đối ở dạng biểu đồ cột hoặc biểu đồ quạt tròn

Tần số tương đối

Bảng tần số tương đối ở dạng bảng ngang

Tần số tương đối thường được viết ở dạng % để không phải quy đồng mẫu mỗi khi so sánh chúng và để thuận tiện cho việc đưa ra dự đoán về một vấn đề, một hiện tượng nào đó liên quan đến mẫu dữ liệu. Khi đó công thức tính tần số tương đối được viết là:

${f_i} = \frac{{{n_i}}}{N}.100\%$

Ví dụ: Cho bảng thống kê số anh, chị, em ruột của các bạn trong lớp:

Tổng số bạn là $n = 30$.

Số anh, chị, em ruột là ${x_1} = 0;{x_2} = 1;{x_3} = 2;{x_4} = 3$ tương ứng với ${m_1} = 8;{m_2} = 12;{m_3} = 6,{m_4} = 4$.

Do đó các tần số tương đối cho các giá trị ${x_1},{x_2},{x_3},{x_4}$ lần lượt là:

${f_1} = \frac{8}{{30}} \approx 26,7\% ;{f_2} = \frac{{12}}{{30}} = 40\% ;{f_3} = \frac{6}{{30}} = 20\% ;{f_4} = \frac{4}{{30}} \approx 13,3\%$.

Ta có bảng tần số tương đối sau:

Lưu ý:

- Trong một mẫu dữ liệu, tổng các tần số tương đối luôn bằng 1 nếu chúng được viết ở dạng thương của ${n_i}$ và $N$, và luôn luôn bằng 100% nếu chúng được viết ở dạng phần trăm.

- Bảng có cả dòng (cột) tần số và dòng (cột) tần số tương đối được gọi là bảng tần số - tần số tương đối.

Nhận xét: Ý nghĩa của tần số tương đối

- Tần số tương đối giúp ta hiểu rõ tỉ lệ xuất hiện nhiều hay ít của mỗi giá trị trong mẫu dữ liệu. Nếu như tần số chỉ cho phép so sánh phân bố của dữ liệu trong cùng một mẫu hay trong hai mẫu, có kích thước bằng nhau thì tần số tương đối là công cụ để so sánh phân bố của dữ liệu trong những mẫu không cùng kích thước.

- Trong thực tiễn, nếu mẫu dữ liệu đại diện được cho tổng thể thì có thể sử dụng tần số tương đối của mẫu để đưa ra một kết luận hay một quyết định cho tổng thể. Điều này không thể làm được nếu chỉ dựa vào tần số.

2. Biểu đồ tần số tương đối

Vẽ biểu đồ tần số ở dạng biểu đồ cột

Vẽ biểu đồ tần số ở dạng biểu đồ hình quạt tròn

Vì đường tròn là cung $360^\circ$ nên hình quạt tròn biểu diễn 1% tương ứng với cung có số đo $\frac{{360^\circ }}{{100}} = 3,6^\circ$. Suy ra hình quạt tròn biểu diễn f% ứng với $f.3,6^\circ$.

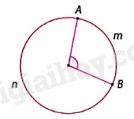
Lưu ý:

- Vì ${f_i} = \frac{{{n_i}}}{N}.100\%$ nên khi có bảng tần số thì ta có thể xác định hình quạt biểu diễn tần số tương đối ${f_i}$ qua cung có số đo $\frac{{{n_i}}}{N}.360^\circ$.

- Để xác định cung khi biết số đo của nó, ta dựa vào tính chất sau: Trong đường tròn, số đo cung nhỏ $\overset\frown{AmB}$ bằng số đo của góc ở tâm chắn cung đó, số đo cung lớn $\overset\frown{AnB}$ bằng hiệu giữa $360^\circ$ và số đo cung $\overset\frown{AmB}$.

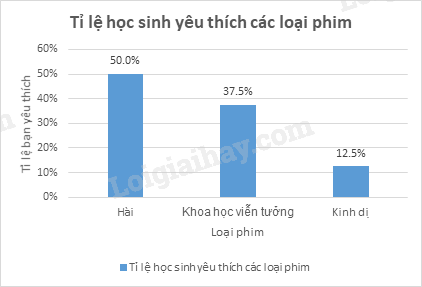
Ví dụ: Cho bảng tần số tương đối về loại phim yêu thích của các học sinh trong lớp 9A như sau:

Biểu đồ tần số tương đối ở dạng biểu đồ cột của mẫu số liệu thống kê đó là:

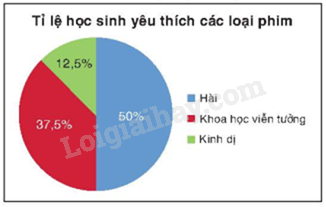
Biểu đồ tần số tương đối ở dạng biểu đồ hình quạt tròn của mẫu số liệu thống kê đó là: