Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá1. Mẫu số liệu ghép nhóm. Tần số ghép nhóm Mẫu số liệu ghép nhóm là một mẫu mà các số liệu đã được ghép với nhau thành từng nhóm, theo một tiêu chí xác định. Các nhóm thường có dạng [a; b), hoặc (a; b], hoặc [a; b]. Hai số a, b được gọi là các mút của nhóm. Nhóm [a; b) (tương ứng: (a; b] hoặc [a; b]) gồm những giá trị x thoả mãn điều kiện a ≤ x < b (tương ứng: a < x < b hoặc a ≤ x < b). Số lần xuất hiện các giá trị thuộc một nhóm được gọi là tần số ghép nhóm của nhóm đó. Mẫu số liệu ghép nhó Quảng cáo
1. Mẫu số liệu ghép nhóm. Tần số ghép nhóm
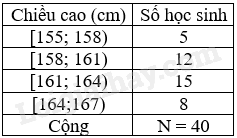
Chú ý: Bảng tần số ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự như trên. Ví dụ: Ta có bảng tần số ghép nhóm cho mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A với các nhóm [155; 158), [158; 161), [161; 164), [164;167) ở dạng bảng ngang:
hoặc ở dạng bảng dọc:
Nhận xét: Việc ghép nhóm số liệu giúp ta trình bày mẫu số liệu được gọn gàng, nhất là với các dãy số liệu liên tục, có nhiều giá trị mà sự phân biệt các giá trị gần bằng nhau lại không cần thiết. Lúc quan sát mẫu số liệu ghép nhóm, thông tin về tần số của mỗi nhóm là yếu tố quan trọng. Lưu ý: Trong nhiều bảng thống kê trên báo chí hoặc Internet, ta có thể gặp cách ghi các nhóm ghép bằng bất đẳng thức. Ví dụ:
Các nhóm (146; 152), [164; 170] trong bảng trên có thể được viết là 146 ≤ h < 152, 164 ≤ h ≤ 170 (với h là chiều cao). 2. Tần số tương đối ghép nhóm
Một bảng có cả tần số ghép nhóm và tần số tương đối ghép tần số được gọi là bảng tần số - tần số tương đối ghép nhóm. 3. Biểu đồ tần số tương đối ghép nhóm dạng cột Để mô tả các bảng tần số tương đối ghép nhóm, ta có thể dùng biểu đồ tần số tương đối ghép nhóm dạng cột (histogram). Cách vẽ:
4. Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng Cách vẽ
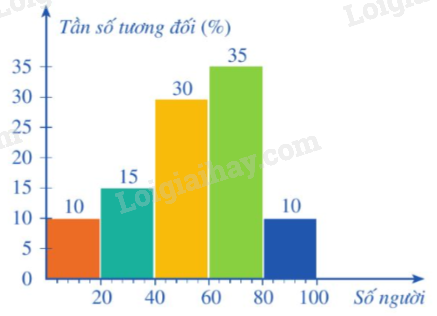
Ví dụ: Bảng tần số tương đối ghép nhóm của mẫu số liệu thống kê số lượng người đến đọc sách trong 100 ngày liên tiếp của một thư viện.
Biểu đồ tần số tương đối ghép nhóm dạng cột của bảng tần số tương đối trên là:
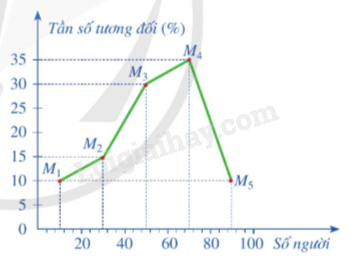
Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng của bảng tần số tương đối trên là:
|























Danh sách bình luận