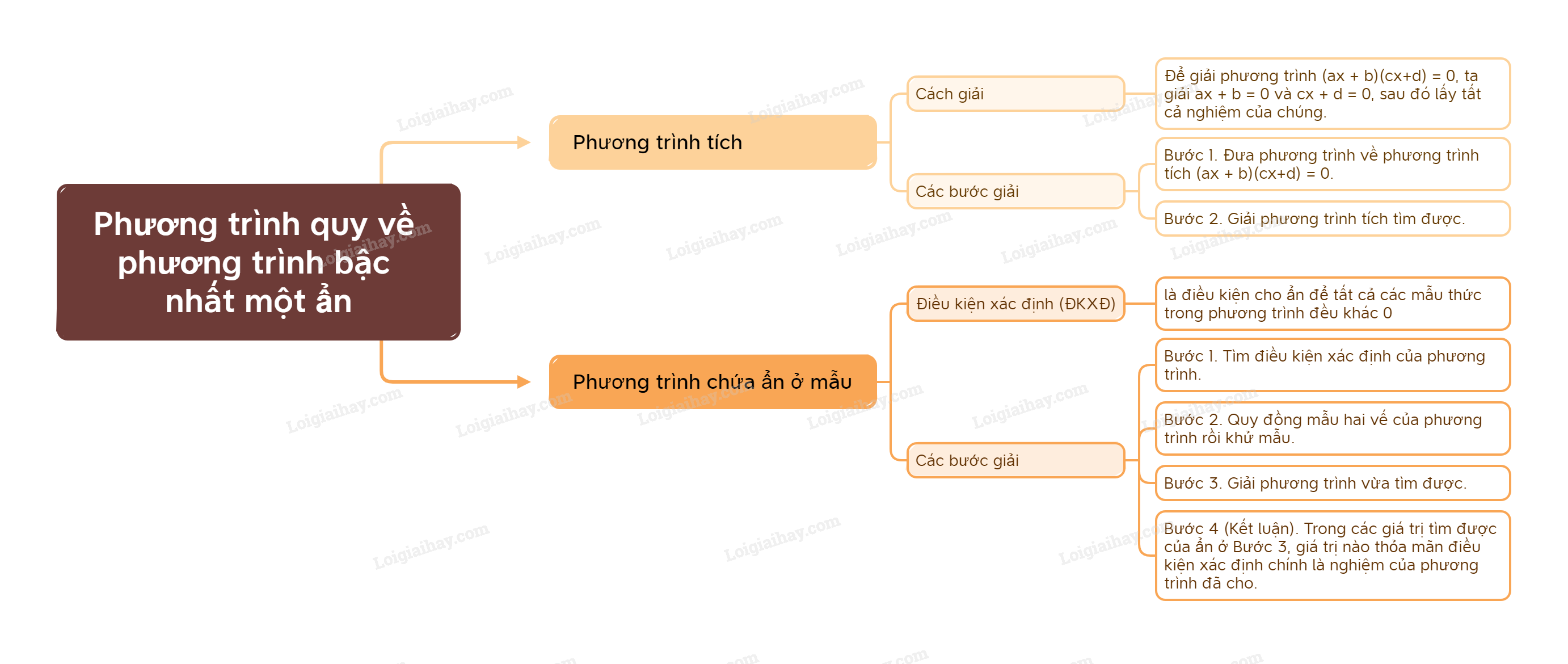
Lý thuyết Phương trình quy về phương trình bậc nhất một ẩn Toán 9 Kết nối tri thức

1. Phương trình tích

Cách giải phương trình tích

Ví dụ: Giải phương trình \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\)

Lời giải:

Ta có: \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\)

nên \(2x + 1 = 0\) hoặc \(3x - 1 = 0\).

\(2x + 1 = 0\) hay \(2x =  - 1\), suy ra \(x =  - \frac{1}{2}\).

\(3x - 1 = 0\) hay \(3x = 1\), suy ra \(x = \frac{1}{3}\).

Vậy phương trình đã cho có hai nghiệm là \(x =  - \frac{1}{2}\) và \(x = \frac{1}{3}\).

Các bước giải phương trình:

Ví dụ: Giải phương trình \({x^2} - x =  - 2x + 2\).

Lời giải:

Biến đổi phương trình đã cho về phương trình tích như sau:

\(\begin{array}{l}{x^2} - x =  - 2x + 2\\{x^2} - x + 2x - 2 = 0\\x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\\left( {x + 2} \right)\left( {x - 1} \right) = 0.\end{array}\)

Ta giải hai phương trình sau:

\(x + 2 = 0\) suy ra \(x =  - 2\).

\(x - 1 = 0\) suy ra \(x = 1\).

Vậy phương trình đã cho có hai nghiệm là \(x =  - 2\) và \(x = 1\).

2. Phương trình chứa ẩn ở mẫu

Điều kiện xác định của phương trình chứa ẩn ở mẫu

Ví dụ:

- Phương trình \(\frac{{5x + 2}}{{x - 1}} = 0\) có điều kiện xác định là \(x \ne 1\) vì \(x - 1 \ne 0\) khi \(x \ne 1\).

- Phương trình \(\frac{1}{{x + 1}} = 1 + \frac{1}{{x - 2}}\) có điều kiện xác định là \(x \ne  - 1\) và \(x \ne 2\) vì \(x + 1 \ne 0\) khi \(x \ne  - 1\), \(x - 2 \ne 0\) khi \(x \ne 2\).

Các bước giải phương trình chứa ẩn ở mẫu

Ví dụ: Giải phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)

Lời giải:

Điều kiện xác định \(x \ne  - 1\) và \(x \ne 2\).

Quy đồng mẫu và khử mẫu, ta được \(\frac{{2\left( {x - 2} \right) + \left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\), suy ra \(2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\).

Giải phương trình \(2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\):

\(\begin{array}{l}2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\\2x - 4 + x + 1 = 3\\3x - 3 = 3\\3x = 6\\x = 2\end{array}\)

Giá trị \(x = 2\) không thỏa mãn ĐKXĐ.

Vậy phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\) vô nghiệm.