Lý thuyết Dấu của tam thức bậc hai - SGK Toán 10 Kết nối tri thứcA. Lý thuyết 1. Dấu của tam thức bậc hai a) Khái niệm tam thức bậc hai Quảng cáo
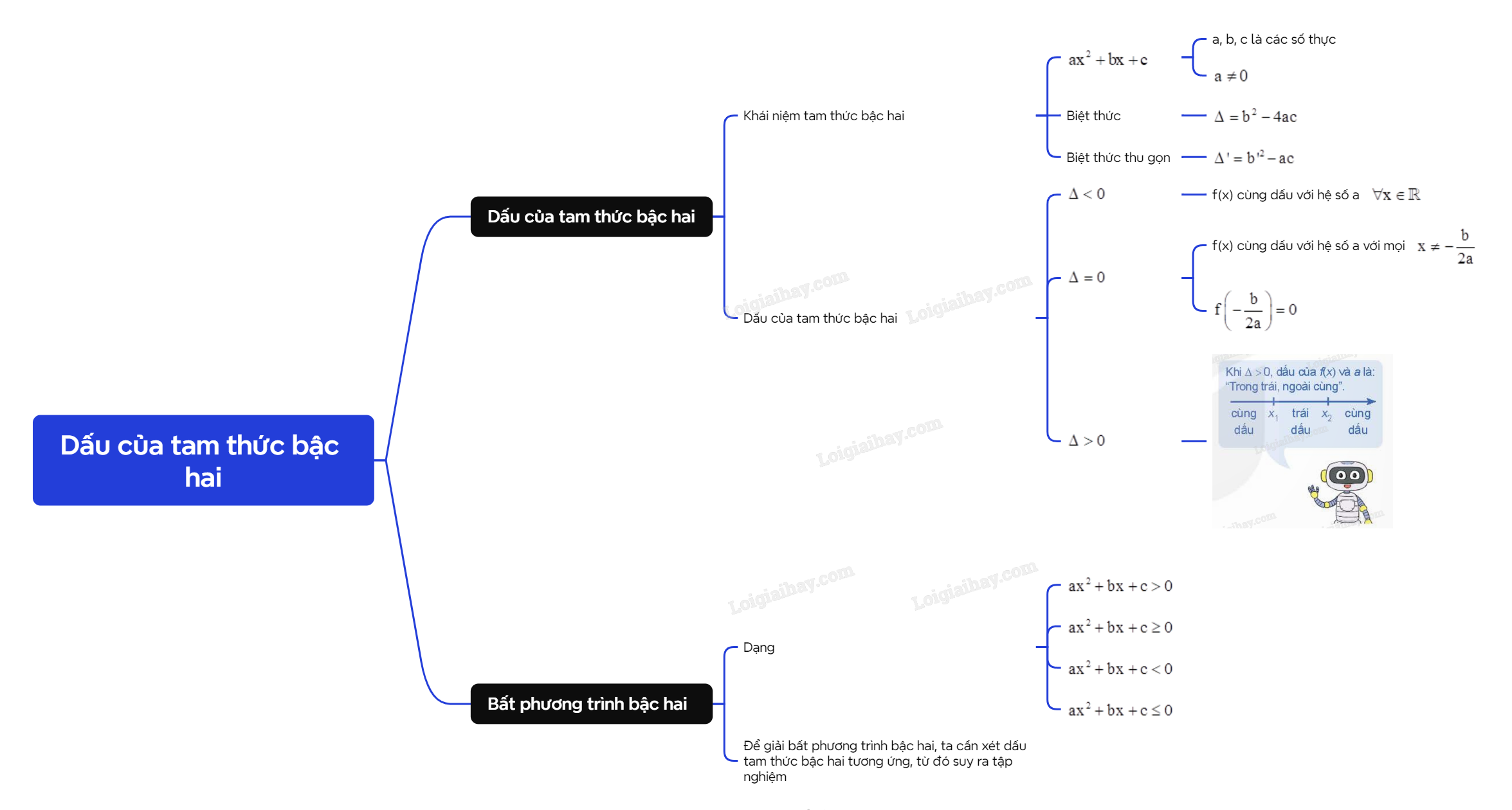
A. Lý thuyết 1. Dấu của tam thức bậc hai a) Khái niệm tam thức bậc hai
Chú ý: Nghiệm của phương trình bậc hai \(a{x^2} + bx + c = 0\) cũng được gọi là nghiệm của tam thức bậc hai \(a{x^2} + bx + c\).
b) Dấu của tam thức bậc hai Mối quan hệ giữa dấu của tam thức bậc hai \(a{x^2} + bx + c\) với dấu của hệ số a trong từng trường hợp của \(\Delta \) được phát biểu trong định lí về dấu của tam thức bậc hai sau đây:
Chú ý: Trong định lí về dấu của tam thức bậc hai, có thể thay \(\Delta \) bởi \(\Delta '\). 2. Bất phương trình bậc hai
Nhận xét: Để giải bất phương trình bậc hai \(a{x^2} + bx + c > 0\) (hoặc \(a{x^2} + bx + c \ge 0\), \(a{x^2} + bx + c < 0\), \(a{x^2} + bx + c \le 0\)) ta cần xét dấu tam thức \(a{x^2} + bx + c\), từ đó suy ra tập nghiệm.
B. Bài tập Bài 1: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai? A. \(3x + 2\sqrt x + 1\) B. \( - 5{x^4} + 3{x^2} + 4\) C. \( - \frac{2}{3}{x^2} + 7x - 4\) D. \({\left( {\frac{1}{x}} \right)^2} + 2\frac{1}{x} + 3\) Giải: \( - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai với \(a = - \frac{2}{3},b = 7,c = - 4\). Bài 2: Xét dấu các tam thức bậc hai sau đây: a) \({x^2} + x + 1\). b) \( - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\). c) \(2{x^2} + 6x - 8\). Giải: a) \(f(x) = {x^2} + x + 1\) có \(\Delta = - 3 < 0\) và \(a = 1 > 0\) nên f(x) > 0 với mọi \(x \in \mathbb{R}\). b) \(f(x) = - \frac{3}{2}{x^2} + 9x - \frac{{27}}{2}\) có \(\Delta = 0\) và \(a = - \frac{3}{2} < 0\) nên f(x) có nghiệm kép x = 3 và f(x) < 0 với mọi \(x \ne 3\). c) Dễ thấy \(f(x) = 2{x^2} + 6x - 8\) có \(\Delta ' = 25 > 0\), a = 2 > 0 và có hai nghiệm phân biệt \({x_1} = - 4\), \({x_2} = 1\). Do đó ta có bảng xét dấu:
Suy ra f(x) > 0 với mọi \(x \in ( - \infty ; - 4) \cup (1; + \infty )\) và f(x) < 0 với mọi \(x \in ( - 4;1)\). Bài 3: Giải các bất phương trình sau: a) \(3{x^2} + x + 5 \le 0\). b) \( - 3{x^2} + 2\sqrt 3 x - 1 \ge 0\). c) \( - {x^2} + 2x + 1 > 0\). Giải: a) Tam thức \(f(x) = 3{x^2} + x + 5\) có \(\Delta = - 59 < 0\), hệ số a = 3 > 0 0 nên f(x) luôn dương (cùng dấu với a) với mọi x, tức là \(3{x^2} + x + 5 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình vô nghiệm. b) Tam thức \(f(x) = - 3{x^2} + 2\sqrt 3 x - 1\) có \(\Delta ' = 0\), hệ số a = -3 < 0 nên f(x) có nghiệm kép \(x = \frac{{\sqrt 3 }}{3}\) và f(x) luôn âm (cùng dấu với a) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\), tức là \( - 3{x^2} + 2\sqrt 3 x - 1 < 0\) với mọi \(x \ne \frac{{\sqrt 3 }}{3}\). Suy ra bất phương trình có nghiệm duy nhất \(x = \frac{{\sqrt 3 }}{3}\). c) Tam thức \(f(x) = - {x^2} + 2x + 1\) có \(\Delta ' = 2 > 0\) nên f(x) có hai nghiệm \({x_1} = 1 - \sqrt 2 \) và \({x_2} = 1 + \sqrt 2 \). Mặt khác, a = -1 < 0, do đó ta có bảng xét dấu sau:
Tập nghiệm của bất phương trình là \(S = \left( {1 - \sqrt 2 ;1 + \sqrt 2 } \right)\).
|






















Danh sách bình luận