Giải bài tập 9.9 trang 76 SGK Toán 9 tập 2 - Kết nối tri thức

Đề bài

Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\widehat {BAH} = \widehat {OAC}\).

Lời giải chi tiết

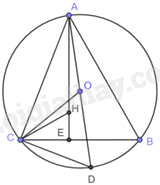
Gọi E là giao điểm của AH và BC nên AE là đường cao của tam giác ABC. Do đó, \(AE \bot BC\)

Suy ra, tam giác BAE vuông tại E nên \(\widehat {EAB} + \widehat B = {90^o}\) hay \(\widehat {BAH} + \widehat B = {90^o}\left( 1 \right)\)

Gọi AD là đường kính của (O). Khi đó, tam giác CAD vuông tại C. Suy ra: \(\widehat {OAC} + \widehat D = {90^o}\left( 2 \right)\)

Vì hai góc B và D là góc nội tiếp cùng chắn cung AC của đường tròn (O; OA) nên \(\widehat B = \widehat D\left( 3 \right)\)

Từ (1), (2) và (3) ta có: \(\widehat {BAH} = \widehat {OAC}\)