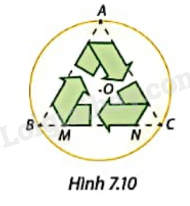
Giải bài tập 7.7 trang 34 SGK Toán 9 tập 2 - Cùng khám pháBiểu tượng tái chế trên thiết kế của huy hiệu hình tròn tam O được bạn Minh dựngDựa trên tam giác đều ABC nội tiếp trong (O) như Hình 7.10. Độ dài cạnh MN của biểu tượng tái chế bằng \(\frac{3}{5}\) độ dài BC. Tính MN nếu đường kính huy hiệu là 4 cm. Làm tròn kết quả đến hàng phần mười centimet. Quảng cáo
Đề bài Biểu tượng tái chế trên thiết kế của huy hiệu hình tròn tam O được bạn Minh dựng dựa trên tam giác đều ABC nội tiếp trong (O) như Hình 7.10. Độ dài cạnh MN của biểu tượng tái chế bằng \(\frac{3}{5}\) độ dài BC. Tính MN nếu đường kính huy hiệu là 4 cm. Làm tròn kết quả đến hàng phần mười centimet.
Phương pháp giải - Xem chi tiết Áp dụng tính chất tam giác đều để tìm bán kính đường tròn Áp dụng định lý Pytago để tìm cạnh của tam giác đều Áp dụng công thức tính diện tích tam giác \(S = \frac{{ah}}{2}\) với ℎ là chiều cao ứng với cạnh đáy là a Lời giải chi tiết
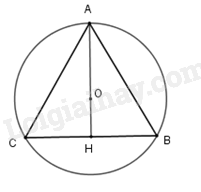
Ta có tam giác ABC đều cạnh a nội tiếp đường tròn (O;R) Khi đó O là trọng tâm tam giác ABC. Gọi AH là đường trung tuyến. Suy ra R = AO = \(\frac{2}{3}\)AH suy ra AH = \(\frac{{3R}}{2}\) Theo định lí Pythagore ta có: AH2 = AB2 – BH2 = \(\frac{{3{a^2}}}{4}\)suy ra AH = \(\frac{{a\sqrt 3 }}{2}\) Từ đó ta có \(\frac{{3R}}{2}\) = \(\frac{{a\sqrt 3 }}{2}\) suy ra a = \(\sqrt 3 \)R. Thay R = \(\frac{4}{2}\)= 2 cm ta được cạnh của tam giác đều BC là: 2\(\sqrt 3 \)cm Suy ra độ dài cạnh MN của biểu tượng tái chế bằng \(\frac{3}{5}\) độ dài BC nên MN = \(\frac{3}{5}\).2\(\sqrt 3 \) = \(\frac{{6\sqrt 3 }}{5} \approx 2,08cm\)
|




















Danh sách bình luận