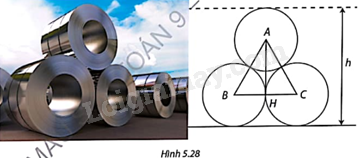
Giải bài tập 5.15 trang 110 SGK Toán 9 tập 1 - Cùng khám pháTrong Hình 5.28, các cuộn thép được đặt chồng lên nhau. Đường kính của mỗi cuộn thép là 1,2m. Gọi A, B, C lần lượt là tâm của mặt cắt các cuộn thép, H là tiếp điểm của hai cuộn thép phía dưới. a) Chứng minh \(\Delta ABC\) là tam giác đều và tính độ dài AH. b) Tính khoảng cách từ B và C đến mặt đất. c) Tính chiều cao h của khối ba cuộn thép. Quảng cáo
Đề bài Trong Hình 5.28, các cuộn thép được đặt chồng lên nhau. Đường kính của mỗi cuộn thép là 1,2m. Gọi A, B, C lần lượt là tâm của mặt cắt các cuộn thép, H là tiếp điểm của hai cuộn thép phía dưới. a) Chứng minh \(\Delta ABC\) là tam giác đều và tính độ dài AH. b) Tính khoảng cách từ B và C đến mặt đất. c) Tính chiều cao h của khối ba cuộn thép.
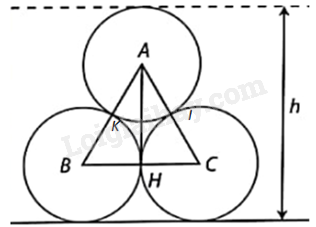
Phương pháp giải - Xem chi tiết a) + Gọi I là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm C, K là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm B. + Tính bán kính của các đường tròn (A), (B), (C). + Từ đó tính được \(AB = BC = AC\) nên tam giác ABC đều. + Chứng minh AH là đường trung tuyến đồng thời là đường cao trong tam giác ABC đều. + Áp dụng định lí Pythagore để tính AH. b) Đường tròn tâm (B), (C) tiếp xúc với mặt đất nên khoảng cách từ B, C đến mặt đất bằng bán kính của đường tròn tâm (B), (C). c) + Chiều cao của ba cuộn thép bằng tổng đường kính của hai đường tròn tâm A và tâm C. Lời giải chi tiết
Gọi I là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm C, K là tiếp điểm của mặt cắt của các cuộn thép tâm A và tâm B. a) Vì AI, AK là bán kính đường tròn (A) nên \(AI = AK = \frac{{1,2}}{2} = 0,6m\). Vì BH, BK là bán kính đường tròn (B) nên \(BH = BK = \frac{{1,2}}{2} = 0,6m\). Vì CI, CH là bán kính đường tròn (C) nên \(CI = CH = \frac{{1,2}}{2} = 0,6m\). Vì các cuộn thép tâm A, B, C đặt chồng lên nhau nên các mặt cắt của các cuộn thép tâm A, B, C tiếp xúc ngoài nhau. Do đó, \(AC = AI + IC = 1,2m,BC = BH + HC = 1,2m,AB = BK + AK = 1,2m\) Suy ra: \(AB = BC = AC\). Vậy \(\Delta ABC\) là tam giác đều Mà AH là đường trung tuyến của tam giác ABC (vì \(BH = HC\)) nên AH là đường cao của tam giác ABC. Suy ra, tam giác AHC vuông tại H. Do đó, \(A{H^2} + H{C^2} = A{C^2}\) (định lí Pythagore), suy ra \(AH = \sqrt {A{C^2} - A{H^2}} = \sqrt {1,{2^2} - 0,{6^2}} = \frac{{3\sqrt 3 }}{5}\left( m \right)\) b) Vì đường tròn tâm (B), (C) tiếp xúc với mặt đất nên khoảng cách từ B, C đến mặt đất bằng bán kính của đường tròn tâm (B), (C). Do đó, khoảng cách từ B và C đến mặt đất đều bằng 0,6m. c) Vì các cuộn thép tâm A, B, C tiếp xúc ngoài nhau nên chiều cao h của khối ba cuộn thép là: \(h = 1,2 + 1,2 = 2,4\left( m \right)\)
|




















Danh sách bình luận