Giải bài tập 4.15 trang 80 SGK Toán 9 tập 1 - Kết nối tri thứcCho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết (HB = 3cm,HC = 6cm,widehat {HAC} = {60^0}.) Hãy tính độ dài các cạnh (làm tròn đến cm) , số đo các góc của tam giác ABC (làm tròn đến độ) . Quảng cáo
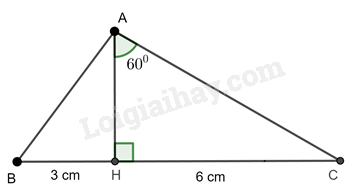
Đề bài Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết \(HB = 3cm,HC = 6cm,\widehat {HAC} = {60^0}.\) Hãy tính độ dài các cạnh (làm tròn đến cm) , số đo các góc của tam giác ABC (làm tròn đến độ) . Video hướng dẫn giải Phương pháp giải - Xem chi tiết Ta cần tính các cạnh AB, BC, CA \(BC = BH + HC\); AC tính dựa vào tỉ số lượng giác của \(\widehat {HAC}\) (\(\sin \widehat {HAC}\) ) Cạnh AB tính thông qua định lý Pythagore trong tam giác vuông ABH, tuy nhiên ta cần tính được cạnh AH, tính cạnh AH thông qua tỉ số lượng giác của \(\widehat {HAC}\left( {\tan \widehat {HAC}} \right)\) Lời giải chi tiết
Cạnh \(BC = BH + HC = 3 + 6 = 9\) cm Ta có: \(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\) hay \(\sin {60^0} = \frac{6}{{AC}}\) hay \(AC = \frac{6}{{\sin {{60}^0}}} = 4\sqrt 3 \approx 7\) cm \(\tan \widehat {HAC} = \frac{{HC}}{{AH}}\) hay \(\tan {60^0} = \frac{6}{{AH}}\) nên \(AH = \frac{6}{{\tan {{60}^0}}} = 2\sqrt 3 \) cm \(\widehat C = 90^\circ - 60^\circ = 30^\circ\) Tam giác ABH vuông tại H nên ta có: \(A{B^2} = A{H^2} + B{H^2} = {\left( {2\sqrt 3 } \right)^2} + {3^2} = 21\) hay \(AB = \sqrt {21} \approx 5\) cm (vì \(AB > 0\)) Ta có: \(tan B = \frac{AH}{BH} = \frac{2\sqrt 3}{3}\) suy ra \( \widehat B \approx 49^\circ\) Áp dụng định lí tổng ba góc trong một tam giác, ta có: \(\widehat {BAC} = 180^\circ - (\widehat B + \widehat C) = 180^\circ - (49^\circ + 30^\circ) = 101^\circ\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
