Giải bài tập 4 trang 124 SGK Toán 9 tập 1 - Cánh diềuChứng minh trong một đường tròn: a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy; b) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy; c) Hai dây bằng nhau thì cách đều tâm; d) Hai dây cách đều tâm thì bằng nhau. Quảng cáo
Đề bài Chứng minh trong một đường tròn: a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy; b) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy; c) Hai dây bằng nhau thì cách đều tâm; d) Hai dây cách đều tâm thì bằng nhau. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào kiến thức đã học để chứng minh. Lời giải chi tiết a)
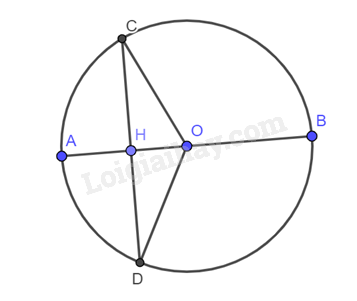
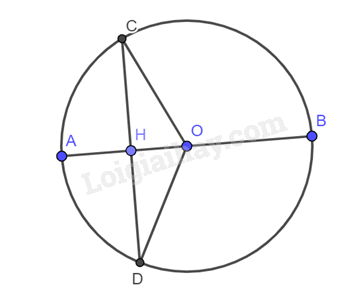
Gọi \(H\) là chân đường vuông góc kẻ từ \(AB\) xuống \(CD\). Do \(AB \bot CD\) nên \(OH \bot CD\). Xét tam giác \(OCD\) có: \(OC = OD \) suy ra \( \Delta OCD\) vuông tại \(O\). Lại có \(OH \bot CD\) nên \(OH\) đồng thời là đường trung tuyến của tam giác \(OCD\). Vậy \(H\) là trung điểm của \(CD\). b)
Gọi \(H\) là trung điểm của \(CD\). Xét tam giác \(OCD\) có: \(OC = OD \) suy ra \( \Delta OCD\) vuông tại \(O\). Lại có \(OH\) là đường trung tuyến của tam giác \(OCD\) nên \(OH\) đồng thời là đường cao của tam giác \(OCD\). Vậy \(OH \bot CD\). c)
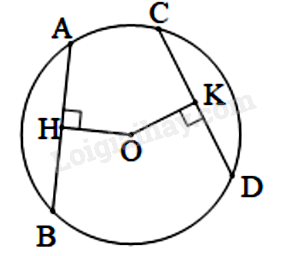
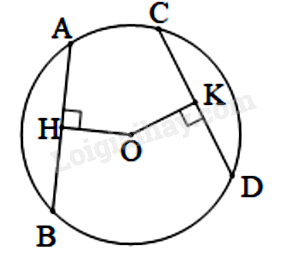
Gọi \(OH,OK\)lần lượt là khoảng cách từ \(O\) tới \(AB,CD\). Do \(AB = CD \Rightarrow AH = CK\). Xét tam giác \(OAH\) và tam giác \(OCK\) có: \(\widehat {AHO} = \widehat {CKO} = 90^\circ \) \(OA = OC = R\) \(AH = CK\) Suy ra \(\Delta AHO = \Delta CKO\) (cạnh huyền – cạnh góc vuông) Do đó \(OH = OK\) (cạnh tương ứng). d)
Gọi \(OH,OK\) lần lượt là khoảng cách từ \(O\) tới \(AB,CD\). Xét tam giác \(OAH\) và tam giác \(OCK\) có: \(\widehat {AHO} = \widehat {CKO} = 90^\circ \) \(OA = OC = R\) \(OH = OK\) Suy ra \(\Delta AHO = \Delta CKO\) (cạnh góc vuông – cạnh góc vuông) Do đó \(AH = CK\) (cạnh tương ứng) Chứng minh tương tự: \(BH = DK\) nên \(AB = CD\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
