Giải bài tập 3 trang 124 SGK Toán 9 tập 1 - Cánh diều

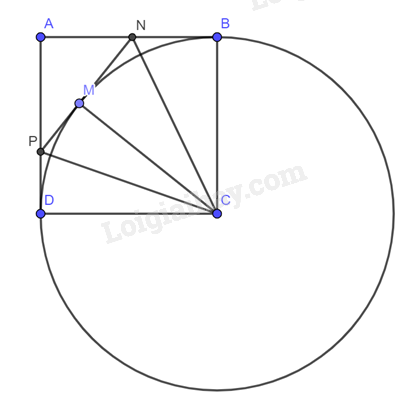
Đề bài

Cho hình vuông \(ABCD\) cạnh \(r\) và đường tròn \(\left( {C;r} \right)\) giả sử \(M\) là một điểm nằm trên đường tròn \(\left( {C;r} \right)\) sao cho điểm \(M\) nằm trong hình vuông \(ABCD\). Tiếp tuyến của đường tròn \(\left( {C;r} \right)\) tại tiếp điểm \(M\) cắt các đoạn thẳng \(AB,AD\) lần lượt tại \(N,P\). Chứng minh:

a) Các đường thẳng \(NB,PD\) là các tiếp tuyến của đường tròn \(\left( {C;r} \right)\).

b) \(\widehat {NCP} = \widehat {NCB} + \widehat {PCD} = 45^\circ \).

Lời giải chi tiết

a) Do \(ABCD\) là hình vuông nên \(AB = BC = CD = AD = r\); \(AB \bot BC\) hay \(NB \bot BC\); \(AD \bot CD\) hay \(PD \bot CD\).

Xét \(\left( C \right)\) có:

+ \(B \in \left( C \right);NB \bot BC \Rightarrow NB\) là tiếp tuyến của \(\left( C \right)\).

+ \(D \in \left( C \right);PD \bot CD \Rightarrow PD\) là tiếp tuyến của \(\left( C \right)\).

b) Do \(MP\) và \(PD\) là hai tiếp tuyến cắt nhau tại \(P\) nên \(CP\) là tia phân giác của \(\widehat {MCD} \Rightarrow \widehat {MCP} = \widehat {PCD}\) (1).

Do \(MN\) nà \(NB\) là hai tiếp tuyến cắt nhau tại \(N\) nên \(CN\) là tia phân giác của \(\widehat {MCB} \Rightarrow \widehat {MCN} = \widehat {BCN}\)(2).

Từ (1) và (2) suy ra \(\widehat {MCP} + \widehat {MCN} = \widehat {PCD} + \widehat {BCN}\) \( \Rightarrow \widehat {PCN} = \widehat {PCD} + \widehat {BCN}\).

Lại có: \(\widehat {PCN} + \widehat {PCD} + \widehat {PCN} = 90^\circ \)  hay \(\widehat {PCN} + \widehat {PCN} = 90^\circ  \Rightarrow \widehat {PCN} = 45^\circ \).

Vậy \(\widehat {PCN} = \widehat {PCD} + \widehat {BCN} = 45^\circ \).