Giải bài tập 2 trang 79 SGK Toán 9 tập 2 - Cánh diềuCho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh (widehat {AIN} = widehat {PMN} = frac{1}{2}widehat {PIN.}) Quảng cáo
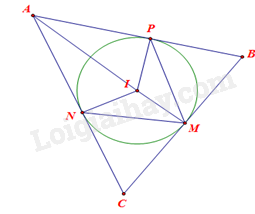
Đề bài Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh \(\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Bước 1: Lý thuyết: Góc ở tâm bằng số đo cung bị chắn, góc nội tiếp bằng một nửa số đo cung bị chắn, suy ra \(\widehat {PMN} = \frac{1}{2}\widehat {PIN.}\) Bước 2: Sử dụng tính chất 2 tiếp tuyến cắt nhau để suy ra \(\widehat {AIN} = \frac{1}{2}\widehat {PIN.}\) Lời giải chi tiết
Xét (I) có: \(\widehat {PIN}\) là góc ở tâm chắc cung NP nên \(\widehat {PIN}\)= sđ\(\overset\frown{NP}\). \(\widehat {PMN}\) là góc nội tiếp chắc cung NP nên \(\widehat {PMN}\) = \(\frac{1}{2}\)sđ\(\overset\frown{NP}\). Suy ra \(\widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)(1) Ta lại có: \(IN \bot AC,IP \bot AB\) nên AB, AC là 2 tiếp tuyến của (I) nên IA là tia phân giác của góc PIN, hay \(\widehat {AIN} = \frac{1}{2}\widehat {PIN.}\)(2) Từ (1) và (2) ta có \(\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
