Giải bài tập 2 trang 117 SGK Toán 9 tập 1 - Cánh diều

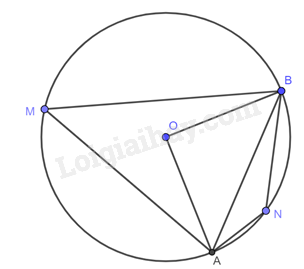
Đề bài

Cho đường tròn \(\left( {O;R} \right)\) và dây \(AB\) sao cho \(\widehat {AOB} = 90^\circ \). Giả sử \(M,N\) lần lượt là các điểm thuộc cung lớn \(AB\) và cung nhỏ \(AB\) (\(M,N\) khác \(A\) và \(B\)).

a) Tính độ dài đoạn thẳng \(AB\) theo \(R\).

b) Tính số đo các góc \(ANB\) và \(AMB\).

Lời giải chi tiết

a) Áp dụng định lí Pythagore vào tam giác \(AOB\) vuông tại \(O\), ta có:

\(O{A^2} + O{B^2} = A{B^2} \Rightarrow A{B^2} = {R^2} + {R^2} = 2{R^2} \Rightarrow AB = R \sqrt 2\)

b) Xét đường tròn \(\left( O \right)\):

+) Vì M thuộc cung lớn AB nên \(\widehat {AMB}\) là góc nội tiếp và \(\widehat {AOB}\) là góc ở tâm cùng chắn cung nhỏ \(AB\) nên:

\(\widehat {AMB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.90^\circ = 45^\circ \).

+) Số đo cung lớn AB là:

$sđ\overset\frown{AB}\; lớn=360{}^\circ - sđ\overset\frown{AB }\; nhỏ=360{}^\circ -90{}^\circ =270{}^\circ $

+) Vì N thuộc cung nhỏ AB nên \(\widehat {ANB}\) là góc nội tiếp chắn cung lớn \(AB\) nên:

$\widehat{ANB}=\frac{1}{2}sđ\overset\frown{AB }\; lớn=\frac{1}{2}.270{}^\circ =135{}^\circ $.

Vậy \(\widehat {AMB} = 45^\circ ,\widehat {ANB} = 135^\circ \).