Giải bài tập 1 trang 92 SGK Toán 9 tập 1 - Cánh diềuCho tam giác (ABC) vuông tại (A) có đường cao (AH) và (widehat B = alpha ) (Hình 40). a) Tỉ số (frac{{HA}}{{HB}}) bằng: A. (sin alpha ). B. (cos alpha ). C. (tan alpha ). D. (cot alpha ). b) Tỉ số (frac{{HA}}{{HC}}) bằng: A. (sin alpha ). B. (cos alpha ). C. (tan alpha ). D. (cot alpha ). c) Tỉ số (frac{{HA}}{{AC}}) bằng: A. (sin alpha ). B. (cos alpha ). C. (tan alpha ). D. (cot alpha ). Quảng cáo
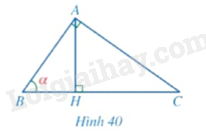
Đề bài Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) và \(\widehat B = \alpha \) (Hình 40).
a) Tỉ số \(\frac{{HA}}{{HB}}\) bằng: A. \(\sin \alpha \). B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \). b) Tỉ số \(\frac{{HA}}{{HC}}\) bằng: A. \(\sin \alpha \). B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \). c) Tỉ số \(\frac{{HA}}{{AC}}\) bằng: A. \(\sin \alpha \). B. \(\cos \alpha \). C. \(\tan \alpha \). D. \(\cot \alpha \). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Dựa vào tỉ số lượng giác để giải bài toán. Lời giải chi tiết a) Chọn đáp án C. b) Xét tam giác \(AHC\) vuông tại \(H\) có: \(\tan C = \frac{{HA}}{{HC}}\). Do \(\widehat B + \widehat C = 90^\circ \) nên \(\tan C = \cot B\). Vậy \(\cot \alpha = \frac{{HA}}{{HC}}\). Chọn đáp án D. c) Xét tam giác \(AHC\) vuông tại \(H\) có: \(\sin C = \frac{{HA}}{{AC}}\). Do \(\widehat B + \widehat C = 90^\circ \) nên \(\sin C = \cos B\). Vậy \(\cos \alpha = \frac{{HA}}{{AC}}\). Chọn đáp án B.
|




















Danh sách bình luận