Bài 82 trang 52 SBT toán 7 tập 2

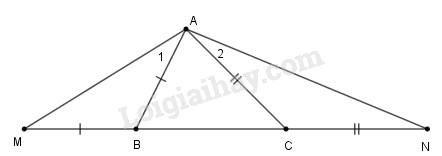
Đề bài

Cho tam giác \(ABC\) có \(AB < AC.\) Trên tia đối của tia \(BC\) lấy điểm \(M\) sao cho \(BM = BA.\) Trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(CN = CA.\)

a) Hãy so sánh các góc \(AMB\) và \(ANC.\)

b) Hãy so sánh các độ dài \(AM\) và \(AN.\)

Lời giải chi tiết

Trong \(∆ABC\) có \(AC > AB\)

\( \Rightarrow \) \(\widehat {ABC} > \widehat {ACB}\) (đối diện cạnh lớn hơn là góc lớn hơn)      (1)

Ta có:   \(AB = BM\) (gt)

\( \Rightarrow ∆ABM\) cân tại \(B\)

\( \Rightarrow \) \(\widehat M = \widehat {{A_1}}\) (tính chất tam giác cân)

Trong \(∆ABM\) ta có có góc ngoài tại đỉnh \(B\) nên \(\widehat {ABC} = \widehat M + \widehat {{A_1}}\)

Suy ra: \(\displaystyle \widehat M = {1 \over 2}\widehat {ABC}\)   (2)

Ta có:   \(AC = CN\) (gt)

\( \Rightarrow ∆CAN\) cân tại \(C\)

\( \Rightarrow \) \(\widehat N = \widehat {{A_2}}\) (tính chất tam giác cân)

Trong \(∆CAN\) ta có \(\widehat {ACB}\) là góc ngoài tại đỉnh \(C.\)

\( \Rightarrow \widehat {ACB} = \widehat N + \widehat {{A_2}}\)

Suy ra: \(\displaystyle \widehat N = {1 \over 2}\widehat {ACB}\)  (3)

Từ (1), (2) và (3) suy ra: \(\widehat M > \widehat N\)

b) Trong \(∆AMN\) ta có: \(\widehat M > \widehat N\)

Suy ra:  \(AN > AM\) (đối diện góc lớn hơn là cạnh lớn hơn)

Loigiaihay.com