Bài 8* trang 102 SBT toán 7 tập 2

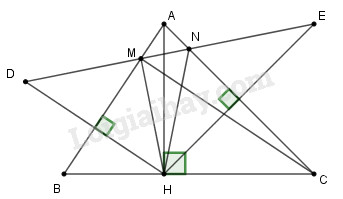
Đề bài

Cho tam giác \(ABC,\) đường cao \(AH.\) Vẽ điểm \(D\) sao cho \(AB\) là đường trung trực của \(HD.\) Vẽ điểm \(E\) sao cho \(AC\) là đường trung trực của \(HE.\) Gọi \(M, N\) theo thứ tự là giao điểm của \(DE\) với \(AB, AC.\) Xét xem các đường thẳng sau là các đường gì trong tam giác \(HMN: MB, NC, HA, HC, MC,\) từ đó hãy chứng minh rằng \(MC\) vuông góc với \(AB.\)

Lời giải chi tiết

Vì \(AB\) là đường trung trực của \(DH\) mà \(M \in AB\) nên \(MD = MH\) hay tam giác \(MDH\) cân tại \(M\) có \(MB\) là đường trung trực nên \(MB\) cũng là đường phân giác \(\widehat {DMH}\).

Mà \(\widehat {DMH}\) là góc ngoài của tam giác \(HMN\) nên \(MB\) là đường phân giác góc ngoài của tam giác \(HMN.\) 

Tương tự: 

Vì \(AC\) là đường trung trực của \(EH\) mà \(N \in AC\) nên \(NH = NE\) hay tam giác \(NEH\) cân tại \(N\) có \(NC\) là đường trung trực nên \(NC\) cũng là đường phân giác \(\widehat {NEH}\).

Mà \(\widehat {NEH}\) là góc ngoài của tam giác \(HMN\) nên \(NC\) là đường phân giác góc ngoài của tam giác \(HMN.\)

Ta lại thấy \(NC\) và \(MB\) cắt nhau tại \(A\) nên \(HA\) là đường phân giác góc trong của tam giác \(HMN\) (hai đường phân giác góc ngoài và một đường phân giác góc trong của tam giác đồng quy tại 1 điểm – Xem bài 9.5 trang 52 SBT toán 7 tập 2)

Lại có: \(HC \bot HA\) tại \(H\) nên \(HC\) là đường phân giác góc ngoài tại đỉnh \(H\) của tam giác \(HMN\) (đường phân giác góc trong và góc ngoài tại 1 đỉnh của 1 tam giác vuông góc với nhau)

Ta thấy \(HC\) và \(NC\) là hai đường phân giác góc ngoài của tam giác \(HNM\) cắt nhau tại \(C\) nên \(MC\) là đường phân giác góc trong của tam giác \(HMN.\)

Như vậy \(MB,MC\) là hai tia phân giác của hai góc \(\widehat {DMH},\widehat {MNH}\) mà hai góc \(\widehat {DMH},\widehat {MNH}\) kề bù nhau nên \(MC \bot MB \Leftrightarrow MC \bot AB.\)

Loigiaihay.com