Bài 6 trang 102 SBT toán 7 tập 2

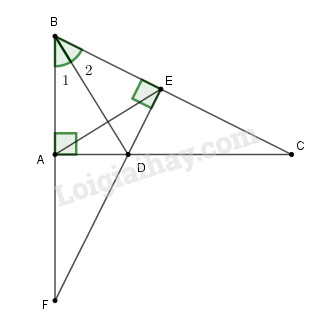
Đề bài

Cho tam giác \(ABC\) vuông tại \(A,\) phân giác \(BD.\) Kẻ \(DE ⊥ BC (E ∈ BC).\) Gọi \(F\) là giao điểm của \(BA\) và \(ED.\) Chứng minh rằng:

a) \(BD\) là đường thẳng trung trực của \(AE;\)

b) \(DF = DC;\)

c) \(AD > DC.\)

Lời giải chi tiết

a) Xét tam giác vuông \(ABD\) và tam giác vuông \(EBD\) có:

+) \(\widehat {{B_1}} = \widehat {{B_2}}\) (do \(BD\) là phân giác góc \(B\))

+) \(BD\) cạnh chung

Suy ra \(\Delta ABD = \Delta EBD\left( {ch - gn} \right)\) nên \(BA = BE;DA = DE\) (các cạnh tương ứng)

Do \(BA = BE\) nên B thuộc đường trung trực của AE.

Do \(DA = DE\) nên D thuộc đường trung trực của AE.

Do đó \(B,D\) cùng thuộc đường trung trực của \(AE\) hay \(BD\) là đường trung trực của \(AE.\)
b) Xét tam giác vuông \(AFD\) và tam giác vuông \(ECD\) có:

+) \(\widehat {ADF} = \widehat {EDC}\) (hai góc đối đỉnh)

+) \(AD = DE\) (theo câu a)

Suy ra \(\Delta AFD = \Delta ECD\left( {g - c - g} \right)\) nên \(DF = DC\) (hai cạnh tương ứng)

c) Xét tam giác vuông \(ADF\) có \(DF\) là cạnh huyền nên \(DF > AD\)

Mà \(DF = DC\) (theo câu b), suy ra \(DC > AD.\)

Loigiaihay.com