Bài 5 trang 102 SBT toán 7 tập 2Bài 5 trang 102 sách bài tập toán 7. Cho tam giác ABC vuông góc tại A, phân giác BD. a) So sánh các độ dài AB và AD; b) So sánh các độ dài BC và BD. Quảng cáo
Đề bài Cho tam giác \(ABC\) vuông góc tại \(A, \) phân giác \(BD.\) a) So sánh các độ dài \(AB\) và \(AD;\) b) So sánh các độ dài \(BC\) và \(BD.\) Phương pháp giải - Xem chi tiết Sử dụng: +) Trong một tam giác: Góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với đỉnh đó +) Trong một tam giác, đối diện với góc lớn hơn là cạnh lớn hơn +) Trong các đường xiên kẻ từ 1 điểm đến 1 đường thẳng: Đường xiên nào có hình chiếu lớn hơn thì lớn hơn. Lời giải chi tiết
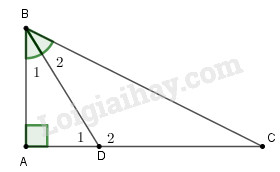
a) Xét tam giác \(BCD\) có \(\widehat {{D_1}}\) là góc ngoài tại đỉnh \(D\) nên \(\widehat {{D_1}} = \widehat {{B_2}} + \widehat C \Rightarrow \widehat {{D_1}} > \widehat {{B_2}}\) Mà \(\widehat {{B_2}} = \widehat {{B_1}}\) (do \(BD\) là phân giác góc \(B\)) nên \(\widehat {{D_1}} > \widehat {{B_1}}\) Xét tam giác \(ABD\) có \(\widehat {{D_1}} > \widehat {{B_1}}\) nên \(AB > AD\) (đối diện với góc lớn hơn là cạnh lớn hơn) b) Cách 1: Hai đường xiên \(BD,BC\) có hai hình chiểu xuống cạnh \(AC\) là \(AD\) và \(AC.\) Mà \(AD < AC \Rightarrow BD < BC\) (quan hệ giữa hình chiếu và đường xiên) Cách 2: Xét tam giác ABD có là \(\widehat {{D_2}}\) là góc ngoài tam giác tại đỉnh D nên: \(\widehat {{D_2}} = \widehat {{B_1}} + \widehat A \Rightarrow \widehat {{D_2}} > \widehat {A}\) Mà \(\widehat {A}=90^0\) nên \(\widehat {{D_2}} > 90^0\) hay \(\widehat {{D_2}} \) là góc tù. Xét tam giác \(ΔBDC\) có \(\widehat {{D_2}} \) là góc tù nên cạnh đối diện với góc \(\widehat {{D_2}} \) là cạnh lớn nhất trong tam giác, hay BC là cạnh lớn nhất của \(ΔBDC\) Do đó \(BC > BD.\) Loigiaihay.com
|














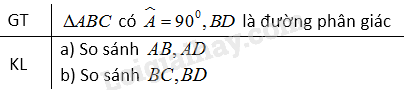






Danh sách bình luận