Bài 6.1, 6.2, 6.3, 6.4 phần bài tập bổ sung trang 47 SBT toán 7 tập 2Giải bài 6.1, 6.2, 6.3, 6.4 phần bài tập bổ sung trang 47 sách bài tập toán 7. Cho tam giác ABC. Trên tia phân giác của góc B, lấy điểm O nằm trong tam giác ABC sao cho O cách đều hai cạnh AB, AC. Khẳng định nào sau đây sai?... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
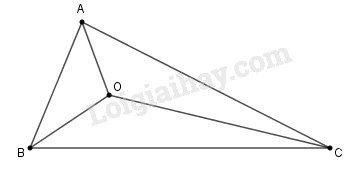
Bài 6.1 Cho tam giác \(ABC.\) Trên tia phân giác của góc \(B,\) lấy điểm \(O\) nằm trong tam giác \(ABC\) sao cho \(O\) cách đều hai cạnh \(AB, AC.\) Khẳng định nào sau đây sai? (A) Điểm \(O\) nằm trên tia phân giác của góc \(A.\) (B) Điểm \(O\) không nằm trên tia phân giác của góc \(C.\) (C) Điểm \(O\) cách đều \(AB, BC.\) (D) Điểm \(O\) cách đều \(AB, AC, BC.\) Phương pháp giải: Sử dụng: +) Điểm cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó. +) Ba đường phân giác trong tam giác cắt nhau tại một điểm. Lời giải chi tiết:
Điểm \(O\) cách đều \(AB, AC\) nên \(O\) thuộc tia phân giác của góc \(A.\) Mặt khác, \(O\) thuộc tia phân giác của góc \(B\) nên \(O\) là giao điểm của ba đường phân giác của tam giác \(ABC.\) Vậy (B) sai còn (A), (C), (D) đúng. Chọn B. Bài 6.2 Cho tam giác \(ABC\) có \(\widehat A = \widehat B + \widehat C\). Hai đường phân giác của góc \(A\) và góc \(C\) cắt nhau tại \(O.\) Khi đó góc \(BOC\) bằng: (A) \(85° ;\) (B) \(90° ;\) (C) \(135° ;\) (D) \(150°.\) Phương pháp giải: Sử dụng: +) Ba đường phân giác của tam giác cắt nhau tại một điểm +) Tổng ba góc trong tam giác bằng \(180^0\) Lời giải chi tiết:
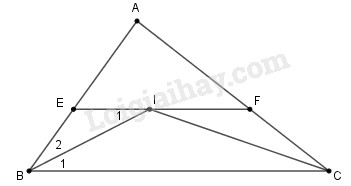
Tam giác \(ABC\) có \(\widehat A + \widehat B + \widehat C=180^0\) (tổng ba góc trong tam giác) mà \(\widehat A = \widehat B + \widehat C\) nên ta có \(\widehat A = \widehat B + \widehat C=\dfrac{180^0}{2}=90^0.\) Lại có \( AO, CO\) lần lượt là tia phân giác của \(\widehat A\) và \(\widehat C\) nên \(BO\) là tia phân giác của \(\widehat B\). Khi đó: \(\displaystyle \widehat {OBC} = {1 \over 2} \widehat B,\) \(\displaystyle \widehat {OCB} = {1 \over 2} \widehat C\) Ta có \(\displaystyle \widehat {OBC} + \widehat {OCB} = {1 \over 2}\left( {\widehat B + \widehat C} \right) \)\(= \dfrac {90^0}{2}=45^\circ \) Xét tam giác \(BOC\) có: \(\widehat {BOC}+\widehat {OBC} + \widehat {OCB} =180^0\) (tổng ba góc trong tam giác) nên \(\widehat {BOC} =180^0-(\widehat {OBC} + \widehat {OCB})\)\(= 180^o-45^o=135^\circ \) Chọn (C). Bài 6.3 Cho tam giác \(ABC.\) Gọi \(I\) là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Qua \(I\) kẻ đường thẳng song song với \(BC\) cắt \(AB, AC\) lần lượt tại \(E\) và \(F.\) Chứng minh rằng \(EF = BE + CF.\) Phương pháp giải: Sử dụng: +) Ba đường phân giác của tam giác cắt nhau tại một điểm. Điểm đó cách đều ba cạnh của tam giác +) Sử dụng tính chất tam giác cân, tính chất hai đường thẳng song song. Lời giải chi tiết:
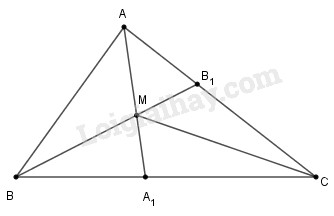
Vì điểm \(I\) cách đều ba cạnh của tam giác \(ABC\) và nằm trong tam giác nên \(I\) là giao điểm của ba đường phân giác của tam giác \(ABC,\) tức là \(BI, CI\) lần lượt là tia phân giác của góc \(B\) và góc \(C.\) Do đó \(\widehat {{B_1}} = \widehat {{B_2}}\) Do \(EF // BC\) nên \(\widehat {{B_1}} = \widehat {{I_1}}\) (so le trong), suy ra \(\widehat {{I_1}} = \widehat {{B_2}}\) Vậy tam giác \(EBI\) cân tại \(E,\) tức là \(EI = EB.\) Lại có \(\widehat {{ICB}} = \widehat {{ICF}}\) (vì CI là tia phân giác góc ACB) Do \(EF // BC\) nên \(\widehat {{FIC}} = \widehat {{ICB}}\) (so le trong), suy ra \(\widehat {{FIC}} = \widehat {{ICF}}\). Vậy tam giác \(FCI\) cân tại \(F,\) tức là \(FI = FC.\) Vậy \(EF = EI + IF = BE + CF.\) Bài 6.4 Hai đường phân giác \({\rm{A}}{{\rm{A}}_1}\) và \(B{B_1}\) của tam giác \(ABC\) cắt nhau tại \(M.\) Hãy tìm các góc \(ACM, BCM\) nếu \({\rm{a}})\widehat {AMB} = 136^\circ \) \(b)\widehat {AMB = }111^\circ \) Phương pháp giải: Sử dụng: +) Ba đường phân giác của tam giác cắt nhau tại một điểm. Điểm đó cách đều ba cạnh của tam giác +) Tổng ba góc trong tam giác bằng \(180^0\) Lời giải chi tiết:
Do ba đường phân giác của một tam giác đồng quy tại một điểm nên \(CM\) là tia phân giác của góc \(C.\) Xét tam giác \(ABC\) có: \(\widehat A + \widehat B +\widehat C=180^0\) (tổng ba góc trong tam giác) nên \(\widehat C=180^0-(\widehat A + \widehat B ) \) a) Xét tam giác \(MAB\), theo định lý về tổng ba góc trong tam giác, ta có: \( \widehat {MAB} + \widehat {MBA} + \widehat {AMB}=180^0\) nên \( \widehat {MAB} + \widehat {MBA} =180^0-\widehat {AMB}\) \( = 180^\circ - 136^\circ = 44^\circ \) Vì AM và BM lần lượt là phân giác của góc A và góc B nên \(\widehat {MAB} =\dfrac{1}{2}\widehat A,\)\( \widehat {MBA} =\dfrac{1}{2}\widehat B\) Xét tam giác \(ABC\) có: \(\displaystyle {1 \over 2}\left( {\widehat A + \widehat B} \right) = \widehat {MAB} + \widehat {MBA} \)\( = 44^\circ \) Suy ra \(\widehat A + \widehat B = 2.44^\circ = 88^\circ \) Nên \(\widehat C=180^0-(\widehat A + \widehat B ) \)\(=180^\circ - 88^\circ = 92^\circ \) Vậy \(\widehat {ACM} = \widehat {BCM} = 92^\circ :2^\circ = 46^\circ \) b) Xét tam giác \(MAB\), theo định lý về tổng ba góc trong tam giác, ta có: \( \widehat {MAB} + \widehat {MBA} + \widehat {AMB}=180^0\) nên \( \widehat {MAB} + \widehat {MBA} =180^0-\widehat {AMB}\) \( = 180^\circ - 111^\circ = 69^\circ \) Vì AM và BM lần lượt là phân giác của góc A và góc B nên \(\widehat {MAB} =\dfrac{1}{2}\widehat A,\)\( \widehat {MBA} =\dfrac{1}{2}\widehat B\) Xét tam giác \(ABC\) có: \(\displaystyle {1 \over 2}\left( {\widehat A + \widehat B} \right) = \widehat {MAB} + \widehat {MBA} \)\( = 69^\circ \). Suy ra \(\widehat A + \widehat B \)\(= 2.69^0=138^\circ \) Suy ra \(\widehat C =180^0-(\widehat A + \widehat B ) \)\(= 180^\circ - 138^\circ = 42^\circ .\) Vậy \(\widehat {ACM} = \widehat {BCM} \)\(= 42^0:2=21^\circ .\) Loigiaihay.com
|























Danh sách bình luận