Bài 53* trang 46 SBT toán 7 tập 2Giải bài 53* trang 46 sách bài tập toán 7. Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi D và E là chân các đường vuông góc kẻ từ I đến AB và AC. a) Chứng minh rằng AD = AE. Quảng cáo
Đề bài Cho tam giác \(ABC\) vuông tại \(A.\) Các tia phân giác của các góc \(B\) và \(C\) cắt nhau tại \(I.\) Gọi \(D\) và \(E\) là chân các đường vuông góc kẻ từ \(I\) đến \(AB\) và \(AC.\) a) Chứng minh rằng \(AD = AE.\) b) Tính các độ dài \(AD, AE\) biết rằng \(AB = 6cm, AC = 8cm.\) Phương pháp giải - Xem chi tiết Sử dụng: +) Tính chất đường phân giác của góc: Các điểm nằm trên đường phân giác của một góc cách đều hai cạnh của góc đó. +) Ba đường phân giác trong tam giác cắt nhau tại một điểm. +) Tính chất hai tam giác bằng nhau Lời giải chi tiết
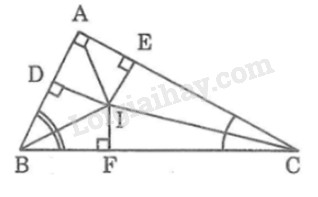
a) Vì \(I\) là giao điểm phân giác trong của \(\widehat B\) và \(\widehat C\) nên \(AI\) là tia phân giác của \(Â.\) \( \Rightarrow ID = IE\) (tính chất tia phân giác) (1) Và \(\widehat {DAI} =\widehat {E{\rm{A}}I}=\dfrac{\widehat {BAC}}{2}\)\(=\dfrac{90^0}{2}= 45^\circ \) (vì \(AI\) là phân giác góc BAC) Vì \(∆ADI \) vuông tại \(D\) có \(\widehat {DAI} = 45^\circ \) Nên \(∆ADI\) vuông cân tại \(D.\) \( \Rightarrow ID = DA\) (2) Vì \(∆AEI\) vuông tại \(E\) có \(\widehat {E{\rm{A}}I} = 45^\circ \) Nên \(∆ AEI\) vuông cân tại \(E\) \( \Rightarrow IE = AE\) (3) Từ (1), (2) và (3) suy ra: \(AD = AE\) b) Trong tam giác vuông \(ABC\) có \( Â=90°\) Theo định lý Pitago ta có: \(\eqalign{ \( \Rightarrow BC = 10 \,(cm)\) Kẻ \(IF \bot BC\) Xét hai tam giác vuông \(IDB\) và \(IFB:\) +) \( \widehat {IDB} = \widehat {IFB} = 90^\circ \) +) Cạnh huyền \(BI\) chung Do đó: \(∆IDB = ∆IFB\) (cạnh huyền - góc nhọn) \( \Rightarrow DB = FB \) (4) (2 cạnh tương ứng) Xét hai tam giác vuông \(IEC\) và \(IFC:\) +) \( \widehat {IEC} = \widehat {IFC} = 90^\circ \) +) Cạnh huyền \(CI\) chung Do đó: \(∆IEC = ∆IFC\) (cạnh huyền - góc nhọn) \( \Rightarrow CE = CF\) (5) Mà \(AD + AE \)\(= AB – DB + AC – CE\) \( \Rightarrow AD + AE \)\(= AB + AC – (DB + CE)\) (6) Từ (4), (5) và (6) suy ra: \(AD + AE = AB + AC – (FB + FC)\)\( = AB + AC – BC\) \(AD + AE = 6 + 8 – 10 = 4\) (cm) Mà \(AD = AE\) (chứng minh trên) \( \Rightarrow AD = AE = 4: 2 = 2 (cm)\)
|














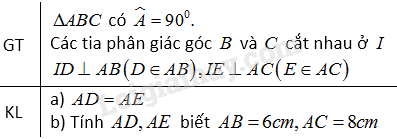






Danh sách bình luận