Bài 46 trang 46 SBT toán 7 tập 2

Đề bài

Cho tam giác \(ABC.\) Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đường thẳng \(AB, BC, CA\) là bằng nhau, đồng thời khoảng cách này là ngắn nhất. 

Lời giải chi tiết

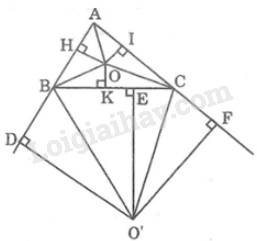
* Nếu \(O\) là điểm nằm trong \(∆ABC\) 

Kẻ \(OH \bot AB,OK \bot BC,OI \bot {\rm{A}}C\)

Vì điểm \(O\) cách đều các đường thẳng \(AB, BC, CA.\)

\( \Rightarrow  OH = OK = OI\) 

Vì \(OH = OK \Rightarrow O\) nằm trên tia phân giác của \(\widehat {ABC}\)

Vì \(OI = OK  \Rightarrow  O\) nằm trên tia phân giác của \(\widehat {ACB}\)

Vì \(OH = OI  \Rightarrow  O\) nằm trên tia phân giác của \(\widehat {BAC}\)

Vậy \(O\) là giao điểm các đường phân giác của  \(∆ABC.\)

* Nếu \(O’\) nằm ngoài \(∆ABC\) 

Kẻ \(O'D \bot AB,O'E \bot BC,O'F \bot {\rm{AC}}\)

\( \Rightarrow  O'D = O'E = O'F\)

Vì \(O'D = O'F  \Rightarrow O\) nằm trên tia phân giác của \(\widehat {BAC}\)

Vì \(O’D = O'E \Rightarrow O'\) nằm trên tia phân giác của \(\widehat {DBC}\)

Vì \(O’F = O'E \Rightarrow O'\) nằm trên tia phân giác của \(\widehat {BCF}\)

\( \Rightarrow O'\) là giao điểm phân giác trong của \(\widehat {BAC}\) và phân giác ngoài tại đỉnh \(B\) và \(C. \) Nên \(A, O, O’\) thẳng hàng ( vì hai tia AO và AO’ đều là tia phân giác trong của góc BAC) và \(A, H, D\) thẳng hàng.

Ta có:  \(OH < O’D\)

Vậy \(O\) là  giao điểm các đường phân giác trong của \(∆ABC\) cách đều ba đường thẳng \(AB, BC, CA\) và khoảng cách này là ngắn nhất.

Loigiaihay.com