Bài 3.9 trang 138 SBT hình học 11

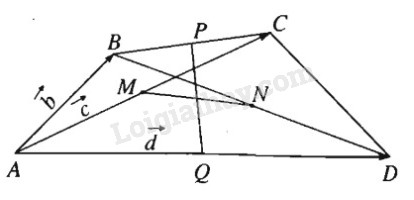
Đề bài

Cho tứ giác $ABCD$. Gọi $M, N, P, Q$ lần lượt là trung điểm của các đoạn $AC, BD, AD$ và có $MN = PQ$. Chứng minh rằng $AB ⊥ CD$.

Lời giải chi tiết

Ta cần chứng minh $\displaystyle \overrightarrow {AB} .\overrightarrow {C{\rm{D}}}  = 0$

Đặt $\displaystyle \overrightarrow {AB}  = \overrightarrow b ,\,\,\overrightarrow {AC}  = \overrightarrow c ,\,\,\overrightarrow {AD}  = \overrightarrow d$. Ta có:

$\displaystyle \overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AN}$ $\displaystyle   =  - {1 \over 2}\overrightarrow {AC}  + {1 \over 2}\left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right)$

Suy ra $\displaystyle \overrightarrow {MN}  = {1 \over 2}\left( {\overrightarrow b  + \overrightarrow d  - \overrightarrow c } \right)$

$\displaystyle \eqalign{ & \overrightarrow {QP} = \overrightarrow {QA} + \overrightarrow {AP} \cr  & = - {1 \over 2}\overrightarrow {A{\rm{D}}} + {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) \cr  & = {1 \over 2}\left( {\overrightarrow b + \overrightarrow c - \overrightarrow d } \right) \cr}$

Theo giả thiết ta có:

$\displaystyle MN = PQ \Leftrightarrow {\overrightarrow {MN} ^2} = {\overrightarrow {QP} ^2}$

$\displaystyle \eqalign{ & {\left( {\overrightarrow b + \overrightarrow d - \overrightarrow c } \right)^2} = {\left( {\overrightarrow b + \overrightarrow c - \overrightarrow d } \right)^2} \cr  & \Leftrightarrow \overrightarrow b .\overrightarrow d - \overrightarrow b .\overrightarrow c = \overrightarrow b .\overrightarrow c - \overrightarrow b .\overrightarrow d \cr  & \Leftrightarrow 2\overrightarrow b .\overrightarrow d - 2\overrightarrow b .\overrightarrow c = 0 \cr  & \Leftrightarrow \overrightarrow b .\left( {\overrightarrow d - \overrightarrow c } \right) = 0 \cr  & \Leftrightarrow \overrightarrow {AB} .\left( {\overrightarrow {A{\rm{D}}} - \overrightarrow {AC} } \right) = 0 \cr  & \Leftrightarrow \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = 0 \Leftrightarrow \overrightarrow {AB} \bot \overrightarrow {C{\rm{D}}} \cr}$

 Loigiaihay.com