Giải bài 3.19 trang 45 SGK Toán 10 tập 1 – Kết nối tri thức

Đề bài

Trên sân bóng chày dành cho nam, các vị trí gôn Nhà (Home plate), gôn 1 (First base), gôn 2 (Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4 m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2, và cách gôn Nhà 18,44 m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.

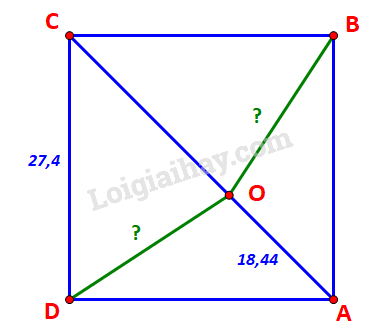
Lời giải chi tiết

Kí hiệu gôn Nhà, gôn 1, gôn 2, gôn 3 và vị trí ném bóng lần lượt là các điểm A, B, C, D, O như hình vẽ.

 

Ta có: 

\(AC = \sqrt {C{D^2} + D{A^2}}  = \sqrt {27,{4^2} + 27,{4^2}}  \approx 38,75\)

\( \Rightarrow OC = AC - OA \approx 38,75 - 18,44 = 20,31\)

Xét tam giác OCD ta có:

Định lí cos: \(O{D^2} = C{D^2} + C{O^2} - 2.CD.CO.\cos C\)

Trong đó \(\left\{ \begin{array}{l}CD = 27,4\\CO = 20,31\\\widehat C = {45^o}\end{array} \right.\)

\(\begin{array}{l} \Rightarrow O{D^2} = 27,{4^2} + 20,{31^2} - 2.27,4.20,31.\cos {45^o}\\ \Leftrightarrow O{D^2} \approx 376,255\\ \Leftrightarrow OD \approx 19,4\;(m)\end{array}\)

Dễ thấy \(\Delta \,COB = \Delta \,COD\) (c.g.c) \( \Rightarrow OB = OD = 19,4\;(m)\)