Giải bài 3.14 trang 44 SGK Toán 10 tập 1 – Kết nối tri thức

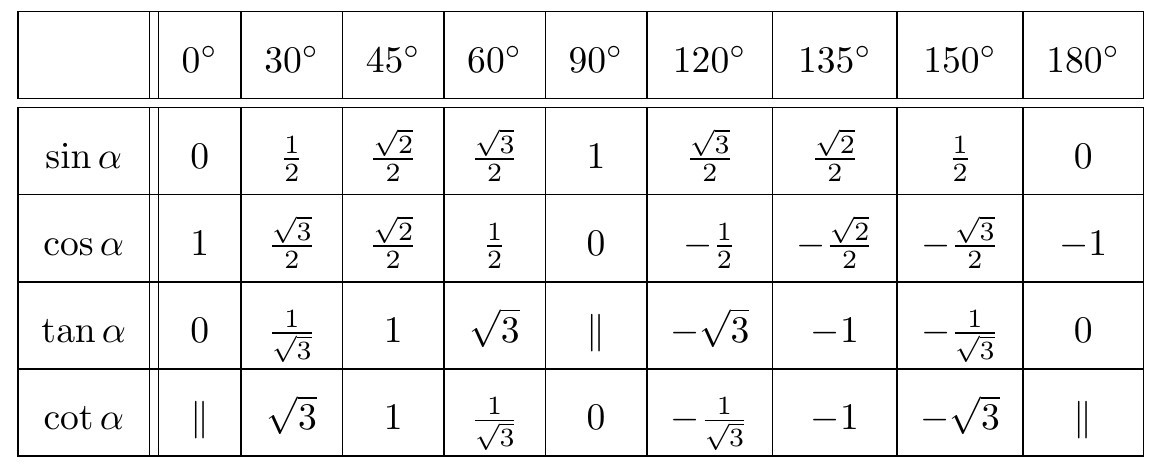
Đề bài

Tính giá trị của các biểu thức sau:

a) \(M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)

b) \(N = \sin {60^o}.\cos {30^o} + \frac{1}{2}.\sin {45^o}.\cos {45^o}\)

c) \(P = 1 + {\tan ^2}{60^o}\)

d) \(Q = \frac{1}{{{{\sin }^2}{{120}^o}}} - {\cot ^2}{120^o}.\)

Lời giải chi tiết

a) \(M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)

Ta có: \(\left\{ \begin{array}{l}\sin {45^o} = \cos {45^o} = \frac{{\sqrt 2 }}{2};\;\\\sin {30^o} = \frac{1}{2}\end{array} \right.\)

Thay vào M, ta được: \(M = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} + \frac{1}{2} = \frac{2}{4} + \frac{1}{2} = 1\)

b) \(N = \sin {60^o}.\cos {30^o} + \frac{1}{2}.\sin {45^o}.\cos {45^o}\)

Ta có: \(\sin {60^o} = \frac{{\sqrt 3 }}{2};\;\;\cos {30^o} = \frac{{\sqrt 3 }}{2};\;\sin {45^o} = \frac{{\sqrt 2 }}{2};\, \cos {45^o}= \frac{{\sqrt 2 }}{2}\)

Thay vào N, ta được: \(N = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{1}{2}.\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = \frac{3}{4} + \frac{1}{4} = 1\)

c) \(P = 1 + {\tan ^2}{60^o}\)

Ta có: \(\tan {60^o} = \sqrt 3 \)

Thay vào P, ta được: \(Q = 1 + {\left( {\sqrt 3 } \right)^2} = 4.\)

d) \(Q = \frac{1}{{{{\sin }^2}{{120}^o}}} - {\cot ^2}{120^o}.\)

Ta có: \(\sin {120^o} = \frac{{\sqrt 3 }}{2};\;\;\cot {120^o} = \frac{{ - 1}}{{\sqrt 3 }}\)

Thay vào P, ta được: \(Q = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}} - \;{\left( {\frac{{ - 1}}{{\sqrt 3 }}} \right)^2} = \frac{1}{{\frac{3}{4}}} - \;\frac{1}{3} = \;\frac{4}{3} - \;\frac{1}{3} = 1.\)