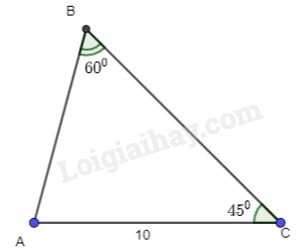
Giải bài 3.15 trang 44 SGK Toán 10 tập 1 – Kết nối tri thức

Đề bài

Cho tam giác ABC có \(\widehat B = {60^o},\;\,\widehat C = {45^o},AC = 10\). Tính \(a,R,S,r\).

Lời giải chi tiết

Theo định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\quad (*)\)

+) Ta có: \(\hat A = {180^o} - \left( {\hat B + \;\hat C} \right) = {180^o} - \left( {{{60}^o} + {{45}^o}} \right) = {75^o}\)

\( \Rightarrow a = \frac{b}{{\sin B}}.\sin A = \frac{{10}}{{\sin {{60}^o}}}.\sin {75^o} \approx 11,154\)

+) \((*) \Rightarrow R = \frac{b}{{2\sin B}} = \frac{{10}}{{2\sin {{60}^o}}} = \frac{{10}}{{2.\frac{{\sqrt 3 }}{2}}} = \frac{{10\sqrt 3 }}{3}.\)

+) Diện tích tam giác ABC là: \(S = \frac{1}{2}ab.\sin {\mkern 1mu} \hat C\) \( \approx \frac{1}{2}.11,154.10.\sin {45^o}\)\( \approx 39,44\)

+) Lại có: \(R = \frac{c}{{2\sin C}}\)\( \Rightarrow c = 2.\frac{{10\sqrt 3 }}{3}.\sin {45^o} = \frac{{10\sqrt 6 }}{3} \approx 8,165\)

\( \Rightarrow p = \frac{{a + b + c}}{2} \approx \frac{{11,154 + 10 + 8,165}}{2} \approx 14,66\)

\( \Rightarrow r = \frac{S}{p} \approx \frac{{39,44}}{{14,66}} \approx 2,7\)