Bài 2.89 trang 109 SBT hình học 10

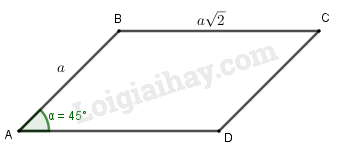
Đề bài

Hình bình hành \(ABCD\) có \(AB = a\), \(BC = a\sqrt 2 \) và \(\widehat {BAD} = {45^0}\). Diện tích hình bình hành bằng:

A. \(2{a^2}\)

B. \({a^2}\sqrt 2 \)

C. \({a^2}\)

D. \({a^2}\sqrt 3 \)

Lời giải chi tiết

Diện tích tam giác \(ABD\) là \({S_{\Delta ABD}} = \dfrac{1}{2}AB.AD.\sin \widehat {BAD}\) \( = \dfrac{1}{2}.a.a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = \dfrac{{{a^2}}}{2}\).

Vậy \({S_{ABCD}} = 2{S_{\Delta ABD}} = 2.\dfrac{{{a^2}}}{2} = {a^2}\).

Chọn C.

Loigiaihay.com