Bài 2.17 trang 91 SBT hình học 10

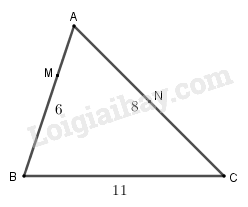
Đề bài

Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 11 cm.

a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \) và chứng tỏ rằng tam giác \(ABC\) có góc \(A\) tù.

b) Trên cạnh AB lấy điểm M sao cho AM = 2 cm và gọi N là trung điểm của cạnh AC. Tính \(\overrightarrow {AM} .\overrightarrow {AN} \).

Lời giải chi tiết

a) Ta có: \(B{C^2} = {\overrightarrow {BC} ^2} = {\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right)^2}\)\( = {\overrightarrow {AC} ^2} + {\overrightarrow {AB} ^2} - 2\overrightarrow {AC} .\overrightarrow {AB} \)

Do đó \(\overrightarrow {AB} .\overrightarrow {AC}  = \dfrac{{{{\overrightarrow {AC} }^2} + {{\overrightarrow {AB} }^2} - {{\overrightarrow {BC} }^2}}}{2}\)\( = \dfrac{1}{2}\left( {{8^2} + {6^2} - {{11}^2}} \right) =  - \dfrac{{21}}{2}\)

\( \Rightarrow AB.AC.cosA =  - \dfrac{{21}}{2}\) \( \Rightarrow \cos A =  - \dfrac{7}{{32}} < 0\) nên \(A\) là góc tù.

b) Ta có \(\overrightarrow {AM}  = \dfrac{1}{3}\overrightarrow {AB} ;\overrightarrow {AN}  = \dfrac{1}{2}\overrightarrow {AC} \)

Do đó \(\overrightarrow {AM.} \overrightarrow {AN}  = \dfrac{1}{3}\overrightarrow {AB} .\dfrac{1}{2}\overrightarrow {AC} \)\( = \dfrac{1}{6}\overrightarrow {AB} .\overrightarrow {AC}  = \dfrac{1}{6}.\left( { - \dfrac{{21}}{2}} \right) =  - \dfrac{7}{4}\)

Loigiaihay.com