Bài 2.19 trang 92 SBT hình học

Đề bài

Cho hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a  + \overrightarrow b } \right| = 13\). Tính tích vô hướng \(\overrightarrow a .(\overrightarrow a  + \overrightarrow b )\) và suy ra góc giữa hai vec tơ \(\overrightarrow a \) và \(\overrightarrow a  + \overrightarrow b \).

Lời giải chi tiết

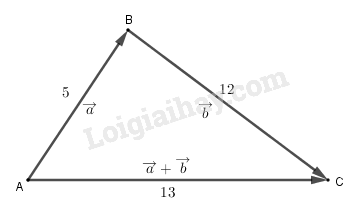
Dựng tam giác ABC có AB = 5, BC= 12 và AC = 13.

Ta có \(\left| {\overrightarrow a } \right| = 5,\left| {\overrightarrow b } \right| = 12\) và \(\left| {\overrightarrow a  + \overrightarrow b } \right| = 13\)

Và \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {BC}  = \overrightarrow b ,\overrightarrow {AC}  = \overrightarrow a  + \overrightarrow b \). Khi đó \(\overrightarrow a (\overrightarrow a  + \overrightarrow b ) = \overrightarrow {AB} .\overrightarrow {AC} \).

Mặt khác ta có:

\(\begin{array}{l}
B{C^2} = {\overrightarrow {BC} ^2} = {\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)^2}\\
= {\overrightarrow {AC} ^2} - 2\overrightarrow {AC} .\overrightarrow {AB} + {\overrightarrow {AB} ^2}\\
= A{C^2} - 2\overrightarrow {AB} .\overrightarrow {AC} + A{B^2}
\end{array}\)

Suy ra \(\overrightarrow {AB} .\overrightarrow {AC}  = \dfrac{1}{2}\left( {A{C^2} + A{B^2} - B{C^2}} \right)\)\( = \dfrac{1}{2}\left( {{{13}^2} + {5^2} - {{12}^2}} \right) = 25\)

Ta suy ra \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}}\)\( = \dfrac{{25}}{{5.13}} \approx 0,3846\)

Suy ra \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) \approx {67^0}{23'}\).

Chú ý :

Có thể nhận xét tam giác \(ABC\) vuông tại \(B\) nên \(\overrightarrow {AB} .\overrightarrow {BC}  = 0\).

Từ đó \(\overrightarrow {AB} .\left( {\overrightarrow {AB}  + \overrightarrow {BC} } \right)\) \( = \overrightarrow {AB} .\overrightarrow {AB}  + \overrightarrow {AB} .\overrightarrow {BC} \) \( = A{B^2} + 0 = 25\).

Loigiaihay.com