Bài 1.52 trang 43 SBT hình học 10Giải bài 1.52 trang 43 sách bài tập hình học 10. Cho lục giác đều ABCDEF và M là một điểm tùy ý. Chứng minh rằng:... Quảng cáo
Đề bài Cho lục giác đều \(ABCDEF\) và \(M\) là một điểm tùy ý. Chứng minh rằng: \(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} \)\( = \overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} \) Phương pháp giải - Xem chi tiết Sử dụng quy tắc trọng tâm \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \) với \(G\) là trọng tâm của \(\Delta ABC\) và \(M\) là một điểm bất kì. Lời giải chi tiết
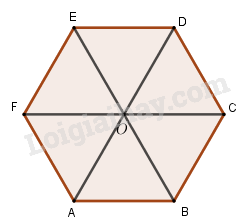
Gọi \(O\) là tâm lục giác đều. Do đó, với mọi điểm \(M\) ta có: \(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = 3\overrightarrow {MO} \) \(\overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} = 3\overrightarrow {MO} \) Vậy ta có đẳng thức cần chứng minh. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
