Bài 1.54 trang 43 SBT hình học 10Giải bài 1.54 trang 43 sách bài tập hình học 10. Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho ... Quảng cáo
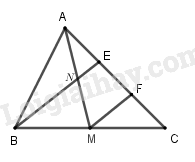
Đề bài Cho tam giác \(ABC\) có trung tuyến \(AM\). Trên cạnh \(AC\) lấy hai điểm \(E\) và \(F\) sao cho \(AE = EF = FC\). \(BE\) cắt trung tuyến \(AM\) tại \( N\). Tính \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} \). Phương pháp giải - Xem chi tiết Dựng hình, thay các véc tơ trong tổng thành các véc tơ bằng nó và thực hiện cộng véc tơ theo quy tắc ba điểm. Lời giải chi tiết
Ta có \(\overrightarrow {AE} = \overrightarrow {FC} \) Vì \(MF // BE\) nên \( N\) là trung điểm của \( AM\), suy ra \(\overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow 0 \) Do đó \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} \)\( = \overrightarrow {AF} + \overrightarrow {FC} = \overrightarrow {AC} \) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
