Bài 1.26 trang 31 SBT hình học 10

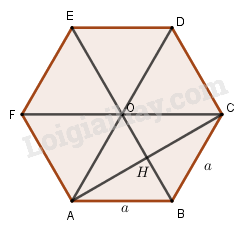
LG a

Phân tích vec tơ \(\overrightarrow {AD} \) theo hai vec tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AF} \).

Phương pháp giải:

Dựng hình và sử dụng các tính chất hình học đã biết để làm bài.

Giải chi tiết:

 \(\overrightarrow {AD}  = 2\overrightarrow {AO}  = 2(\overrightarrow {AB}  + \overrightarrow {AF} )\) \( = 2\overrightarrow {AB}  + 2\overrightarrow {AF} \)

LG b

 Tính độ dài của vec tơ \(\dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {BC} \) theo \(a\).

Phương pháp giải:

Dựng hình và sử dụng các tính chất hình học đã biết để làm bài.

Giải chi tiết:

\(\dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {BC}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {BC} } \right) = \dfrac{1}{2}\overrightarrow {AC} \)\( \Rightarrow \left| {\dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {BC} } \right| = \dfrac{1}{2}\left| {\overrightarrow {AC} } \right|\)

Dễ thấy tam giác \(OAB\) đều có \(AH = \sqrt {A{B^2} - B{H^2}} \) \( = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\)

Tứ giác \(AOCB\) là hình thoi nên \(AC = 2AH = a\sqrt 3 \).

Vậy  \(\left| {\dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {BC} } \right| = \dfrac{1}{2}\left| {\overrightarrow {AC} } \right| = \dfrac{{a\sqrt 3 }}{2}\).

Loigiaihay.com