Bài 1.30 trang 32 SBT hình học 10Giải bài 1.30 trang 32 sách bài tập hình học 10. Cho tam giác ABC... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
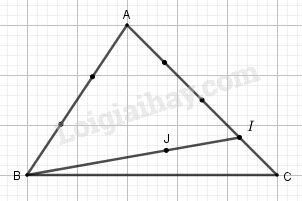
Cho tam giác \(ABC\). Điểm \(I\) trên cạnh \(AC\) sao cho \(CI = \dfrac{1}{4}CA\), \(J\) là điểm mà \(\overrightarrow {BJ} = \dfrac{1}{2}\overrightarrow {AC} - \dfrac{2}{3}\overrightarrow {AB} \). LG a Chứng minh \(\overrightarrow {BI} = \dfrac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} \). Phương pháp giải: Xen điểm và biểu diễn các véc tơ thích hợp. Lời giải chi tiết:
\(\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} = - \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {AC} \) LG b Chứng minh \(B, I, J\) thẳng hàng. Phương pháp giải: Chứng minh \(\overrightarrow {BJ} = k\overrightarrow {BI} \). Lời giải chi tiết: Ta có: \(\begin{array}{l} Vậy ba điểm \(B, J, I\) thẳng hàng. LG c Hãy dựng điểm \(J\) thỏa mãn điều kiện đề bài. Phương pháp giải: Dựng hình dựa vào ý b. Lời giải chi tiết: Do \(\overrightarrow {BJ} = \dfrac{2}{3}\overrightarrow {BI} \) nên ta dựng được hình như hình vẽ trên. Loigiaihay.com
|




















Danh sách bình luận